
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
【答案】(1)点E是线段AD的中点.(2)2.
【解析】
(1)由AC=BD易知AB=CD,再由E是线段BC的中点可知BE=CE,则AE=AB+BE=CD+EC=ED,故点E是线段AD的中点;
(2)由上问所得E是AD中点及AD=10可得AE=5,再由AB=3可得BE=AE-AB=5-3=2.
解:(1)点E是线段AD的中点.理由如下:
∵AC=BD,
∴AB+BC=BC+CD,
∴AB=CD.
∵E是线段BC的中点;
∴BE=EC,
∴AB+BE=CD+EC,即AE=ED,
∴点E是线段AD的中点.
(2)∵E是AD中点,AD=10,
∴AE=![]() AD=
AD=![]() ×10=5,
×10=5,
∴BE=AE-AB=5-3=2,
即线段BE的长度为2.


科目:初中数学 来源: 题型:
【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
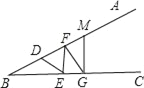
【题目】已知:如图,BD=DE=EF=FG.
(1)若∠ABC=20°,∠ABC内符合条件BD=DE=EF=FG的折线(如DE、EF、FG)共有几条?若∠ABC=10°呢?试一试,并简述理由.
(2)若∠ABC=m°(0<m<90),你能找出一个折线条数n与m之间的关系吗?若有,请找出来;若无,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,李敏发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38①,
然后在①式的两边都乘3,得3S=3+32+33+34+35+36+37+38+39②
②-①得,3S-S=39-1,即2S=39-1,
所以S=![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母a(a≠0且a≠1),能否求出1+a+a2+a3+a4+…+a2 017的值?如能求出,其正确答案是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A=2x2+ax﹣5y+b,B=bx2﹣![]() x﹣
x﹣![]() y﹣3.
y﹣3.
(1)求3A﹣(4A﹣2B)的值;
(2)当x取任意数值,A﹣2B的值是一个定值时,求(a+![]() A)﹣(2b+
A)﹣(2b+![]() B)的值.
B)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
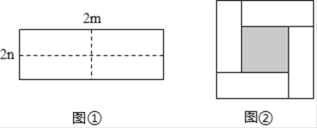
【题目】图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形.
(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一:S小正方形= ;
方法二:S小正方形= ;
(2)(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系为
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求x﹣y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘上1、2、3、4四个数字分别代表鸡、猴、鼠、羊四种生肖邮票(每种邮票各两枚,鸡年邮票面值“80分”,其它邮票都是面值“1.20元”),转动转盘后,指针每落在某个数字所在扇形一次就表示获得该种邮票一枚. 
(1)任意转动转盘一次,获得猴年邮票的概率是;
(2)任意转动转盘两次,求获得的两枚邮票可以邮寄一封需2.4元邮资的信件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com