
【题目】如图,△ABD中,∠BAD=90°,AB=AD,△ACE中,∠CAE=90°,AC=AE。
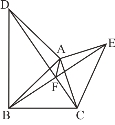
(1)求证:DC=BE;
(2)试判断∠AFD和∠AFE的大小关系,并说明理由。
【答案】(1)证明见解析;(2)∠AFD=∠AFE.理由见解析.
【解析】
试题分析:(1)求出∠DAC=∠BAE,根据SAS得出△DAC≌△BAE,即可得出结论;
(2)根据全等三角形的性质得出两三角形面积相等和DC=BE,根据面积公式求出AM=AN,根据角平分线的判定方法即可得出结论.
试题解析:(1)∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
又AD=AB,AC=AE,
∴△DAC≌△BAE(SAS),
∴DC=BE.
(2)∠AFD=∠AFE,理由如下:
过A作AM⊥DC于M,AN⊥BE于N,如图所示:
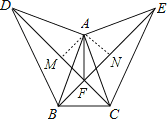
∵△DAC≌△BAE,
∴S△ACD=S△ABE,DC=BE,
∴![]() DC×AM=
DC×AM=![]() BE×AN,
BE×AN,
∴AM=AN,
∴点A在∠DFE的平分线上,
∴∠AFD=∠AFE.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
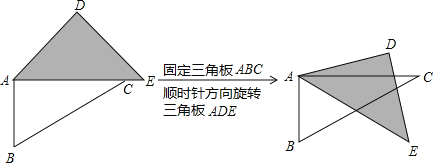
【题目】如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).当△ADE的一边与△ABC的某一边平行(不共线)时,写出旋转角α的所有可能的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
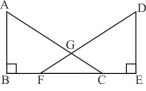
求证:(1)△ABC≌△DEF;
(2)GF=GC。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )
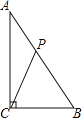
A.5 B.5或8 C.![]() D.4或
D.4或![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com