
【题目】在平面直角坐标系中,O(0,0)、B(a,b),且a、b满足1﹣2a+a2+(b![]() )2=0.
)2=0.
(1)求a,b的值;
(2)若点A在x轴正半轴上,且OA=2,在平面内有一动点Q(不在x轴上),QO=m,QA=n,QB=p,且p2=m2+n2,求∠OQA的度数.
(3)阅读以下内容:对于实数a、b有(a﹣b)2≥0,∴a2﹣2ab+b2≥0,
即a2+b2≥2ab.
利用以上知识,在(2)的条件下求△AOQ的面积的最大值.
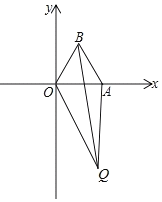
【答案】(1)a=1,b![]() ;(2)∠OQA的度数为30°或150°;(3)当∠OQA=30°时,△AOQ的面积的最大值为2
;(2)∠OQA的度数为30°或150°;(3)当∠OQA=30°时,△AOQ的面积的最大值为2![]() ;当∠OQA=150°时,△AOQ的面积的最大值为2
;当∠OQA=150°时,△AOQ的面积的最大值为2![]() .
.
【解析】
(1)由题意根据完全平方式的非负性,即可求得a和b的值;
(2)根据题意易证△OAB为等边三角形,故可通过把△ABQ绕点A逆时针旋转60°得△AOC,把已知的QO=m、QA=n、QB=p统一到△OCQ中,得到△OCQ是直角三角形,再加上旋转得到的∠AQC=60°,即能求出∠OQA的度数;但由于不确定点Q的位置,故需分点Q在△OAB内部和点Q在△OAB外部两种情况讨论计算;
(3)由题意通过构造OQ边上的高AH求得△AOQ面积的表达式,根据条件给的不等式可知,当a=b时,ab可取得最大值为a2+b2,即OQ=AQ时,△AOQ取得最大值;根据勾股定理把AQ=OQ求出,即求出面积最大值;由于在(2)的条件下不确定∠OQA的度数,故需分两种情况讨论计算.
解:(1)∵1﹣2a+a2+(b![]() )2=0,
)2=0,
∴(1﹣a)2+(b![]() )2=0,
)2=0,
∴1﹣a=0,b![]() 0,
0,
∴a=1,b![]() .
.
(2)∵OA=2即A(2,0),B(1,![]() ),
),
∴OB![]() ,AB
,AB![]() ,
,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠OAB=60°,
把△ABQ绕点A逆时针旋转60°得△AOC,连接CQ,
∴∠CAQ=∠OAB=60°,AC=AQ=n,OC=BQ=p,
∴△ACQ是等边三角形,
∴CQ=AQ=n,∠AQC=60°,
∵p2=m2+n2即OC2=OQ2+CQ2,
∴△OCQ是直角三角形,∠OQC=90°,
①若点Q在△OAB的外部,如图1,
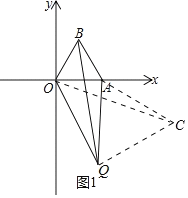
则∠OQA=∠OQC﹣∠AQC=90°﹣60°=30°;
②若点Q在△OAB的内部,如图2,
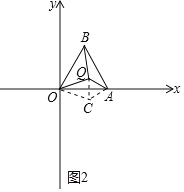
则∠OQA=∠OQC+∠AQC=90°+60°=150°,
综上所述:∠OQA的度数为30°或150°.
(3)∵a2+b2≥2ab,
∴当a=b时,a2+b2=2ab成立,即此时ab取得最大值,
过点A作AH⊥OQ于H,如图3,
∴∠AHQ=90°,
∵∠AQH=30°,
∴AH![]() AQ
AQ![]() n,
n,
∴S△AOQ![]() OQAH
OQAH![]() m
m![]() n
n![]() mn,
mn,
∴当m=n时,S△AOQ取得最大值![]() ,
,
①当∠OQA=30°时,如图3.
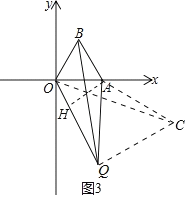
∵OQ=AQ=n,QH![]() ,
,
∴OH=OQ﹣QH=n![]() n,
n,
∵OA=2,OA2=OH2+AH2,
∴(n![]() n)2+(
n)2+(![]() n)2=22,
n)2=22,
解得:n2=4(2![]() ),
),
∴S△AOQ![]() n2=2
n2=2![]() ;
;
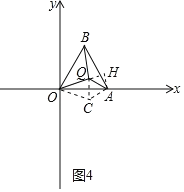
②当∠OQA=150°时,如图4,
∴OH=OQ+QH=n![]() n,
n,
∵OA=2,OA2=OH2+AH2,
∴(n![]() n)2+(
n)2+(![]() n)2=22,
n)2=22,
解得:n2=4(2![]() ),
),
∴S△AOQ![]() n2=2
n2=2![]() ,
,
综上所述:当∠OQA=30°时,△AOQ的面积的最大值为2![]() ;
;
当∠OQA=150°时,△AOQ的面积的最大值为2![]() .
.


科目:初中数学 来源: 题型:
【题目】(8分)现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再抽取一张.
(1)求两次抽得相同花色的概率;
(2)当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)
查看答案和解析>>
科目:初中数学 来源: 题型:
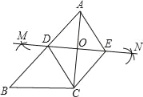
【题目】如图,已知△ABC,按如下步骤作图:
①分别以A、C为圆心,以大于![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形;
(2)当∠ACB=90°,BC=6,△ADC的周长为18时,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0,![]() ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC为等边三角形,O为BC的中点,D、E分别在边AB、AC上.如图1.
(1)若∠DOE=120°,求证:OD=OE;
(2)如图2,BD=4,CE=2,M是DE的中点,求OM的长.
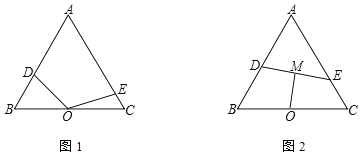
查看答案和解析>>
科目:初中数学 来源: 题型:
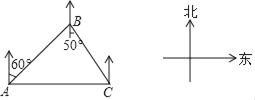
【题目】如图,淇淇一家驾车从A地出发,沿着北偏东60°的方向行驶,到达B地后沿着南偏东50°的方向行驶来到C地,C地恰好位于A地正东方向上,则( )
①B地在C地的北偏西50°方向上;
②A地在B地的北偏西30°方向上;
③cos∠BAC=![]() ;
;
④∠ACB=50°.其中错误的是( )
A. ①② B. ②④ C. ①③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=2∠B.
(1)作∠ACB的平分线交AB于D(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)若AB=10,AC=6,求△ACD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
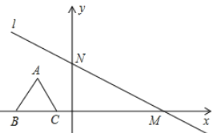
【题目】如图,在平面直角坐标系中,有一条直线l:y=![]() +4与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移
+4与x轴、y轴分别交于点M、N,一个高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移
(1)在平移过程中,得到△A1B1C1,此时顶点A1恰落在直线l上,写出A1点的坐标;
(2)继续向右平移,得到△A2B2C2,此时△A2B2C2的三边中垂线的交点P(即外心)恰好落在直线l上,求P点的坐标;
(3)在直线l上是否存在这样的点,与(2)中的A2、B2、C2任意两点能同时构成三个等腰三角形?如果存在,求出点的坐标;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com