

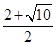 ,?
,?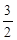 );(3)P点的坐标为(
);(3)P点的坐标为(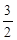 ,?
,?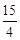 ),四边形ABPC的面积的最大值为
),四边形ABPC的面积的最大值为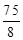 .
.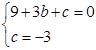 ,解得:
,解得: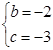 ;
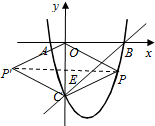
;
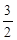
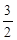 ;
;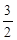
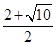 ,x2=
,x2=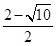 (不合题意,舍去),
(不合题意,舍去),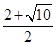 ,?
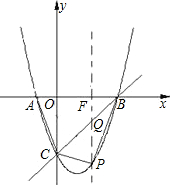
,?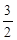 )
)
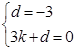 ,解得:
,解得: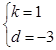
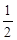 AB•OC+
AB•OC+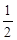 QP•BF+
QP•BF+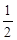 QP•OF
QP•OF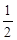 ×4×3+
×4×3+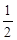 (?x2+3x)×3
(?x2+3x)×3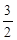 (x?
(x?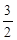 )2+
)2+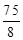
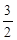 时,四边形ABPC的面积最大
时,四边形ABPC的面积最大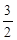 ,?
,?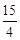 ),四边形ABPC的面积的最大值为
),四边形ABPC的面积的最大值为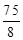


 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
|
如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为( ) 
|
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
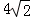 ,则△EFC的周长为
,则△EFC的周长为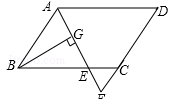
| A.11 | B.10 | C.9 | D.8 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+ ;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
A.2 011+671 | B.2 012+671 |
C.2 013+671 | D.2 014+671 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com