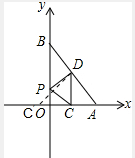
解(1)∵y=kx+b过A(2,0),B(0,4),
∴将点A、B的坐标代入y=kx+b得,
k=-2,b=4,
∴解析式为:y=-2x+4;
当x=1时,y=-2×1+4=2,所以点在函数图象上.
(2))△PCD的面积不发生变化;
∵A(2,0),B(0,4),C、D是线段OA、AB的中点,
∴C(1,0)、D(1,2),
∴CD=2,
又∵点P在y轴上运动,CD∥y轴,
∴点P到y轴的距离总是1,及△PCD的CD边上的高为n=1,
∴三角形PCD的面积s=

CD.h=

×2×1=1,
∴△PCD的面积不发生变化;
(3)△PCD的周长发生变化.
∵0(0,0),A(2,0),且C为AO的中点,
∴点C的坐标为(1,0),
则C关于y轴的对称点为C′(-1,0),
又∵B(0,4),A(2,0)且D为AB的中点,
∴点D的坐标为(1,2),
连接C′D,设C′D的解析式为y=kx+b,
则

,
解得:
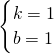
,
∴y=x+1是DC′的解析式,
∵x=0,∴y=1,
即P(0,1).
∵PC+PD的最小值=C′D,
∴由勾股定理得C′D=2

,
∵△PCD的周长的最小值为C′D+CD,CD=2,
∴△PCD的周长的最小值为

+2;
(4)P(0,1)或P(0,

)或P(0,

)或P(0,

)或P(0,

).
故答案为:y=-2x+4.
分析:(1)将点A、B的坐标代入y=kx+b并计算出k、b的值,从而得出解析式,然后验证(1,2)是否在函数图象上即可;
(2)根据点A、B的坐标和C、D是线段OA、AB的中点,得出点C和D的坐标,求出CD的长,再根据CD∥y轴,得出点P到y轴的距离以及△PCD的CD边上的高,从而求出三角形PCD的面积,即可得出△PCD的面积不发生变化;
(3)根据题意先取点C关于点O的对称点为C′,连接DC′,即C′、P、D共线时,PC+PD的最小值是C′D,再根据△PCD的周长的最小值为C′D+CD,在直角三角形C′CD中,根据勾股定理,可得C′D的长,根据三角形的中位线定理已知点P的坐标,即可得出C′D的值,再根据CD=2,即可求出△PCD的周长的最小值.
(4)根据题目中所给的条件,即可得出点P的坐标,共有5种情况,使△PCD为等腰三角形.
点评:本题考查了一次函数的综合应用及最短路线问题,用到的知识点是待定系数法求一次函数的解析式,两点之间线段最短的定理以及勾股定理的运用,本题有一定的难度,注意第(4)问点P有五种情况,不要漏项.

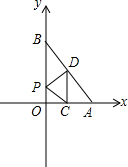 一次函数y=kx+b的图象与x、y轴分别交于点A(2,0)、B(0,4),O为坐标系原点,线段OA、AB的中点分别为点C、D,P为直线OB上一动点,
一次函数y=kx+b的图象与x、y轴分别交于点A(2,0)、B(0,4),O为坐标系原点,线段OA、AB的中点分别为点C、D,P为直线OB上一动点, 解(1)∵y=kx+b过A(2,0),B(0,4),
解(1)∵y=kx+b过A(2,0),B(0,4), CD.h=
CD.h= ×2×1=1,
×2×1=1, ,
,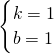 ,
, ,
, +2;
+2; )或P(0,
)或P(0, )或P(0,
)或P(0, )或P(0,
)或P(0, ).
).

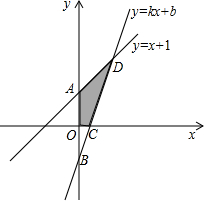 x轴以及y=x+1的图象分别交于点C、D.
x轴以及y=x+1的图象分别交于点C、D. (2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,
(2013•潍坊)如图,抛物线y=ax2+bx+c关于直线x=1对称,与坐标轴交与A,B,C三点,且AB=4,点D(2,