
【题目】如图1,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4)

(1)求B点坐标;
(2)如图2,若C为x正半轴上一动点,以AC为直角边作等腰直角△ACD,∠ACD=90°,连接OD,求∠AOD的度数;
(3)如图3,过点A作y轴的垂线交y轴于E,F为x轴负半轴上一点,G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过A作x轴垂线交EH于点M,连FM,等式AM=FM+OF是否成立?若成立,请说明;若不成立,说明理由.
【答案】(1)B(8,0);(2)90°;(3)AM=FM+OF成立,理由见解析.
【解析】试题分析:(1)作AE⊥OB于E,因为△AOB为等腰直角三角形,A(4,4),则B点坐标可求;
(2)作AE⊥OB于E,DF⊥OB于F,求证△DFC≌△CEA,再根据等量变换,即可求出∠AOD的度数可求;
(3)在AM上截取AN=OF,连EN,易证△EAN≌△EOF,再根据角与角之间的关系,证明△NEM≌△FEM,则有AM-MF=OF,即可求证等式成立.
试题解析:(1)如图所示,作AE⊥OB于E,
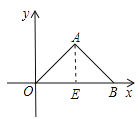
∵A(4,4),
∴OE=4,
∵△AOB为等腰直角三角形,且AE⊥OB,
∴OE=EB=4,
∴OB=8,
∴B(8,0);
(2)如图所示,作AE⊥OB于E,DF⊥OB于F,
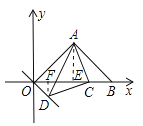
∵△ACD为等腰直角三角形,
∴AC=DC,∠ACD=90°
即∠ACF+∠DCF=90°,
∵∠FDC+∠DCF=90°,
∴∠ACF=∠FDC,
又∵∠DFC=∠AEC=90°,
∴△DFC≌△CEA(AAS),
∴EC=DF,FC=AE,
∵A(4,4),
∴AE=OE=4,
∴FC=OE,即OF+EF=CE+EF,
∴OF=CE,
∴OF=DF,
∴∠DOF=45°,
∵△AOB为等腰直角三角形,
∴∠AOB=45°,
∴∠AOD=∠AOB+∠DOF=90°;
(3)AM=FM+OF成立,理由:
如图所示,在AM上截取AN=OF,连EN.
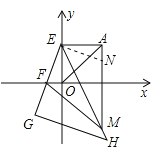
∵A(4,4),
∴AE=OE=4,
又∵∠EAN=∠EOF=90°,AN=OF,
∴△EAN≌△EOF(SAS),
∴∠OEF=∠AEN,EF=EN,
又∵△EGH为等腰直角三角形,
∴∠GEH=45°,即∠OEF+∠OEM=45°,
∴∠AEN+∠OEM=45°
又∵∠AEO=90°,
∴∠NEM=45°=∠FEM,
又∵EM=EM,
∴△NEM≌△FEM(SAS),
∴MN=MF,
∴AM﹣MF=AM﹣MN=AN,
∴AM﹣MF=OF,
即AM=FM+OF.


科目:初中数学 来源: 题型:
【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x | 20 | 25 | 30 | 50 |
销售量y | 15 | 12 | 10 | 6 |
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,
(1)请判断线段AE和BD的数量关系和位置关系,并证明;
(2)若已知∠AED=135°,设∠AEC=α,当△BDE为等腰三角形时,求α的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】圆的周长公式C=2πR中,下列说法正确的是( )
A.π、R是自变量,2是常量 B.C是因变量,R是自变量,2π为常量
C.R为自变量,2π、C为常量 D.C是自变量,R为因变量,2π为常量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊数学家把数1,3,6,10,15,21,…叫做三角形数,其中1是第一个三角形数,3是第2个三角形数,6是第3个三角形数,…依此类推,那么第9个三角形数是 , 2016是第 个三角形数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.
(1)求证:AC·CD=CP·BP;
(2)若AB=10,BC=12,当PD∥AB时,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四句话中的文字有三句具有对称规律,其中没有这种规律的一句是( )
A.上海自来水来自海上
B.保卫diao1yu1dao
C.清水池里池水清
D.蜜蜂酿蜂蜜
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com