
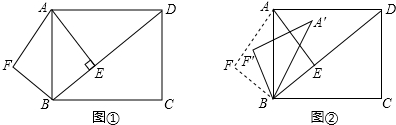
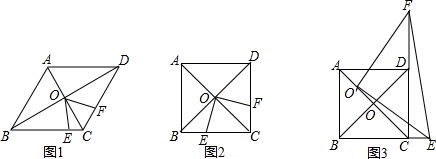
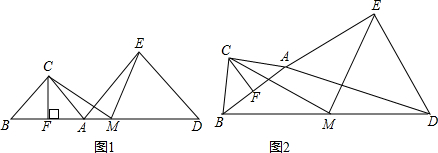
���� ��1�����þ������ʡ����ɶ����������������ʽ��⣻
��2�������⻭��ͼ�Σ����ͼ2��ʾ������ƽ�����ʣ�ȷ��ͼ���еĵ��������Σ��ֱ����m��ֵ��
��3������ת�����У�������DPQ��4�����Σ����ͼ3��ʾ�����ڸ������ηֱ���м��㣮
��� �⣺��1����Rt��ABD�У�AB=5��AD=$\frac{20}{3}$��
�ɹ��ɶ����ã�BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=$\sqrt{{5}^{2}+��\frac{20}{3}��^{2}}$=$\frac{25}{3}$��
��S��ABD=$\frac{1}{2}$BD•AE=$\frac{1}{2}$AB•AD��
��AE=$\frac{AB•AD}{BD}$=$\frac{5��\frac{20}{3}}{\frac{25}{3}}$=4��
��Rt��ABE��AB=5��AE=4��
�ɹ��ɶ����ã�BE=3��
��2����ƽ���е�������Ϊ��A��B��F�䣬���ͼ2��ʾ��
�ɶԳƵ����ʿ�֪����1=��2��
��ƽ�����ʿ�֪��AB��A��B�䣬��4=��1��BF=B��F��=3��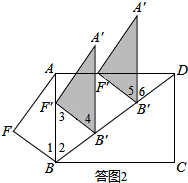
�ٵ���F������AB��ʱ��
��AB��A��B�䣬
���3=��4��
���3=��2��
��BB��=B��F��=3����m=3��
�ڵ���F������AD��ʱ��
��AB��A��B�䣬
���6=��2��
�ߡ�1=��2����5=��1��
���5=��6��
����֪A��B���AD��
���B��F��D����������
��B��D=B��F��=3��
��BB��=BD-B��D=$\frac{25}{3}$-3=$\frac{16}{3}$����m=$\frac{16}{3}$��
��3�����ڣ��������£�
����ת�����У�������DPQ����������4�����Σ�
�����ͼ3-1��ʾ����Q����BD�ӳ����ϣ���PD=DQ����֪��2=2��Q��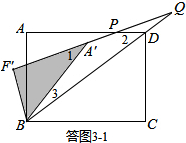
�ߡ�1=��3+��Q����1=��2��
���3=��Q��
��A��Q=A��B=5��
��F��Q=F��A��+A��Q=4+5=9��
��Rt��BF��Q�У��ɹ��ɶ����ã�BQ=$\sqrt{F��{Q}^{2}+F��{B}^{2}}$=$\sqrt{{9}^{2}+{3}^{2}}$=3$\sqrt{10}$��
��DQ=BQ-BD=3$\sqrt{10}$-$\frac{25}{3}$��
�����ͼ3-2��ʾ����Q����BD�ϣ���PQ=DQ����֪��2=��P��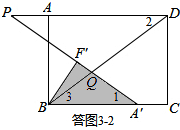
�ߡ�1=��2��
���1=��P��
��BA���PD�����ʱ��A������BC���ϣ�
�ߡ�3=��2��
���3=��1��
��BQ=A��Q��
��F��Q=F��A��-A��Q=4-BQ��
��Rt��BQF���У��ɹ��ɶ����ã�BF��2+F��Q2=BQ2��
����32+��4-BQ��2=BQ2��
��ã�BQ=$\frac{25}{8}$��
��DQ=BD-BQ=$\frac{25}{3}$-$\frac{25}{8}$=$\frac{125}{24}$��
�����ͼ3-3��ʾ����Q����BD�ϣ���PD=DQ����֪��3=��4��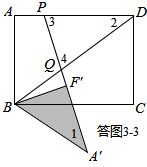
�ߡ�2+��3+��4=180�㣬��3=��4��
���4=90��-$\frac{1}{2}$��2��
�ߡ�1=��2��
���4=90��-$\frac{1}{2}$��1��
���A��QB=��4=90��-$\frac{1}{2}$��1��
���A��BQ=180��-��A��QB-��1=90��-$\frac{1}{2}$��1��
���A��QB=��A��BQ��
��A��Q=A��B=5��
��F��Q=A��Q-A��F��=5-4=1��
��Rt��BF��Q�У��ɹ��ɶ����ã�BQ=$\sqrt{F��{Q}^{2}+F��{B}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$��
��DQ=BD-BQ=$\frac{25}{3}$-$\sqrt{10}$��
�����ͼ3-4��ʾ����Q����BD�ϣ���PQ=PD����֪��2=��3��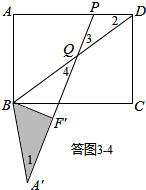
�ߡ�1=��2����3=��4����2=��3��
���1=��4��
��BQ=BA��=5��
��DQ=BD-BQ=$\frac{25}{3}$-5=$\frac{10}{3}$��
��������������4����������ĵ�P����Q��ʹ��DPQΪ���������Σ�
DQ�ij��ȷֱ�Ϊ3$\sqrt{10}$-$\frac{25}{3}$��$\frac{125}{24}$��$\frac{25}{3}$-$\sqrt{10}$��$\frac{10}{3}$��
���� �����Ǽ��α任ѹ���⣬�漰��ת��ƽ�Ʊ任�����Ρ����ɶ��������������ε�֪ʶ�㣮�ڣ�3�����ѶȺܴ���ؼ��ǻ���������תͼ�Σ���������з������ۣ��ڼ�������У�ע��ʶ����ת�����еIJ�������ע�����õ��������ε����ʼ��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ij�����������ͼ��������ݣ��������ж���ȷ���ǣ�������
��ͼ����ij�����������ͼ��������ݣ��������ж���ȷ���ǣ�������| A�� | a��c | B�� | b��c | C�� | a2+4b2=c2 | D�� | a2+b2=c2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
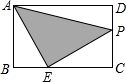 ��ͼ���ھ���ABCD�У�AB=2��AD=3����E��BC����һ�㣬��BE=1������P�ӵ�A��������·��A��D��C��E�˶������APE�����y���P������·�̳�x֮��ĺ�����ϵ��ͼ���ʾӦΪ��������
��ͼ���ھ���ABCD�У�AB=2��AD=3����E��BC����һ�㣬��BE=1������P�ӵ�A��������·��A��D��C��E�˶������APE�����y���P������·�̳�x֮��ĺ�����ϵ��ͼ���ʾӦΪ��������| A�� |  | B�� |  | C�� | 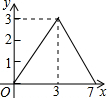 | D�� | 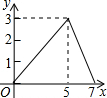 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1���෴����1 | B�� | -1����С�ĸ����� | ||
| C�� | -1�ľ���ֵ��1 | D�� | -1�����ĸ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
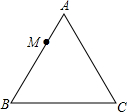 ��ͼ����M�ӵȱ������εĶ���A��������ֱ�������˶�����B������ֱ�������˶�����C�������������У���M��A�ľ���Ϊy����M���˶�ʱ��Ϊx����ôy��x��ͼ�����Ϊ��������
��ͼ����M�ӵȱ������εĶ���A��������ֱ�������˶�����B������ֱ�������˶�����C�������������У���M��A�ľ���Ϊy����M���˶�ʱ��Ϊx����ôy��x��ͼ�����Ϊ��������| A�� |  | B�� | 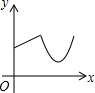 | C�� | 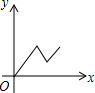 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{3}{4}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com