
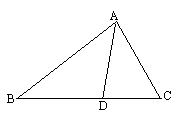
如图,AD是△ABC的角平分线,AB=AC+DC.求证:∠C=2∠B.
|
证明:已知中的“形”,主要是线段或角的倍数、和差关系.如此题在已知中有“AB=AC+DC”,如何在图形中转化这个条件?想到作辅助线最常见的作法“截长补短法”,又由∠BAD=∠CAD,想到利用这两个角之间的相等关系构造两个全等的三角形,于是可把△ACD沿AD翻折得△AED,或将△ABD沿AD翻折得△ACF.
在AB上截取AE=AC,连结DE(即把△ACD沿AD翻折得△AED),在△AED和△ACD中 AE=AC,∠EAD=∠CAD,AD=AD ∴△AED≌△ACD ∴DE=CD,∠C=∠AED. 又∵AB=AC+DC=AE+DC=AE+BE ∴DE=BE ∴∠B=∠EDB ∴∠C=∠AED=∠B+∠EDB=2∠B. |


科目:初中数学 来源: 题型:
 如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.
如图,AD是△ABC的边BC上的中线,已知AB=5cm,AC=3cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com