
 实数a,b在数轴上的位置如图所示,且|a|>|b|,化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$=b.
实数a,b在数轴上的位置如图所示,且|a|>|b|,化简:$\sqrt{{a}^{2}}$-$\sqrt{(a+b)^{2}}$=b.  期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,OC是∠AOB内部的一条射线,且OM,ON分别平分∠AOC与∠BOC.
如图,OC是∠AOB内部的一条射线,且OM,ON分别平分∠AOC与∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=$\frac{1}{2}$,cot∠ABC=$\frac{3}{4}$,AD=8.
如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=$\frac{1}{2}$,cot∠ABC=$\frac{3}{4}$,AD=8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| a1,1 | a1,2 | a1,3 | a1,4 |
| a2,1 | a2,2 | a2,3 | a2,4 |
| a3,1 | a3,2 | a3,3 | a3,4 |
| a4,1 | a4,2 | a4,3 | a4,4 |
| 问题1 | 问题2 |
| a2,1•ai,j+a2,2•ai,j+a2,3•ai,j+a2,4•ai,j=0或3; | 表中的16个数中,共有10个1. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
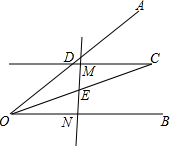 如图,∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.
如图,∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com