Question

16．如图，△ABC内接于⊙O，BD为⊙O的直径，BD与AC相交于点H，AC的延长线与过点B的直线相交于点E，且∠A=∠EBC，作CG∥EB，CG与BD、BA分别相交于点F、G，下列说法中：①CF⊥BD；②BC²=BG•BA；③BC²=BF•BD；④CH=CB．正确的个数是 （　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 连接CD，由BD是直径，得到∠BCD=90°，即∠D+∠CBD=90°，根据平行线的性质得到CF⊥BD，故①正确；根据相似三角形的判定和性质得到BC²=BG•BA；故②正确；根据相似三角形的判定和性质得到BC²=BF•BD，故③正确；由现有条件得不到CH=CB，故④错误．．

解答 解：连接CD，
∵BD是直径，
∴∠BCD=90°，即∠D+∠CBD=90°，
∵∠A=∠D，∠A=∠EBC，
∴∠CBD+∠EBC=90°，
∴BE⊥BD，
∵CG∥EB，
∴CF⊥BD，故①正确；
∵CG∥EB，
∴∠BCG=∠EBC，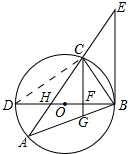
∴∠A=∠BCG，
∵∠CBG=∠ABC
∴△ABC∽△CBG，
∴$\frac{BC}{BG}=\frac{AB}{BC}$，即BC²=BG•BA；故②正确；
∵CG∥EB，
∴CF⊥BD，
∴△BFC∽△BCD，
∴BC²=BF•BD，故③正确；
由现有条件得不到CH=CB，故④错误．
故选C．

点评 本题考查了相似三角形的判定和性质，圆周角定理，正确的作出辅助线是解题的关键．