
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ�����������������ǵ��ճ������У���ˣ�Խ��Խ�����ϲ�������г����У�ij���г���������ij�ͺ����г�ʱ���Ը߳����۵�50%��ۣ���֪����۾������۸��ͺ����г�8���뽫���ֱ��100Ԫ����7��������ͬ��
��1������ͺ����г��Ľ��ۺͱ�۷ֱ��Ƕ���Ԫ��
��2�������ͺ����г��Ľ��۲��䣬����1���еı�۳��ۣ��õ�ƽ��ÿ�¿��۳�50������ÿ�����г�ÿ����20Ԫ��ÿ�¿ɶ��۳�5��������ͺ����г����۶���Ԫʱ��ÿ�¿ɻ���30000Ԫ��
���𰸡���1�����ͺ����г��Ľ���Ϊ1000Ԫ�����Ϊ1500Ԫ����2�����ͺ����г�����100Ԫ��200Ԫʱ��ÿ�¿ɻ���30000Ԫ��
��������
��1������ͺ����г��Ľ���ΪxԪ������Ϊ��1+50%��xԪ�����������ۼ۩����۽�ϰ���۾������۸��ͺ����г�8���뽫���ֱ��100Ԫ����7��������ͬ�����ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��2������ͺ����г�����yԪ����ƽ��ÿ�¿��۳���50+![]() y����������������ÿ�����������������������ɵó�����y��һԪ���η��̣���֮���ɵó����ۣ�
y����������������ÿ�����������������������ɵó�����y��һԪ���η��̣���֮���ɵó����ۣ�
�⣺��1������ͺ����г��Ľ���ΪxԪ������Ϊ��1+50%��xԪ��
�����⣬�ã�8��[0.9����1+50%��x��x]��7��[��1+50%��x��100��x]��
��ã�x��1000��
����1+50%��x��1500��
�𣺸��ͺ����г��Ľ���Ϊ1000Ԫ�����Ϊ1500Ԫ��
��2������ͺ����г�����yԪ����ƽ��ÿ�¿��۳���50+![]() y������
y������
�����⣬�ã���1500��1000��y����50+![]() y����30000��
y����30000��
�������ã�y2��300y+20000��0��
��ã�y1��100��y2��200��
�𣺸��ͺ����г�����100Ԫ��200Ԫʱ��ÿ�¿ɻ���30000Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
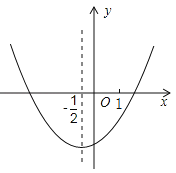
����Ŀ����֪���κ���![]() ͼ����ͼ��ʾ���Գ���Ϊ����
ͼ����ͼ��ʾ���Գ���Ϊ����![]() ��ƽ����
��ƽ����![]() ���ֱ�ߣ������н�������ȷ���ǣ� ��
���ֱ�ߣ������н�������ȷ���ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
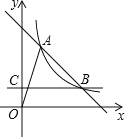
����Ŀ����ͼ��ֱ��y��4��x��˫����y![]() ����A��B���㣬��B��ֱ��BC��y�ᣬ����ΪC������OAΪֱ����Բ��ֱ��BC�Ľ���������_____��
����A��B���㣬��B��ֱ��BC��y�ᣬ����ΪC������OAΪֱ����Բ��ֱ��BC�Ľ���������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳:���ۺ�ʵ�����ϣ���ʦ��ͬѧ����������ֽƬ�ļ�ƴ��Ϊ���չ��ѧ�����ͼ��1������һ������ֽƬABCD����BAD��60�����ضԽ���AC�������õ���ABC����ACD
��������:��1����ͼ��1���е���ABC��AΪ��ת���ģ�˳ʱ�뷽����ת������0��������60�����õ���ͼ��2����ʾ��ABC�����ֱ��ӳ�BC����DC���ڵ�E������CE��C��E������֤��������ۣ�
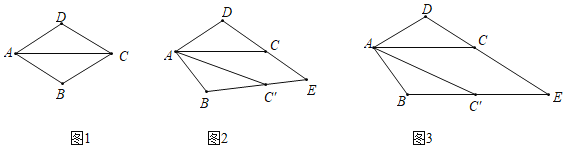
��2�������⣨1���Ļ����ϣ�����ת�������ڶ��ٶ�ʱ���ı���ACEC�������Σ���������ͼ��3��˵�����ɣ�
��չ̽��:��3�����������⣨2���Ļ����ϣ�����C����C��F��AC����DC���ڵ�F�����ж�AD��DF��AC��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
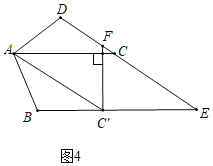
����Ŀ����ͼ����һ�ž���ֽƬABCD�У�AB=4��BC=8����E��F�ֱ���AD��BC�ϣ���ֽƬABCD��ֱ��EF�۵�����C����AD�ϵ�һ��H������D���ڵ�G�����������ĸ����ۣ�
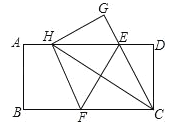
���ı���CFHE�����Σ�
��ECƽ�֡�DCH��
���߶�BF��ȡֵ��ΧΪ3��BF��4��
�ܵ���H���A�غ�ʱ��EF=2![]() ��
��
���Ͻ����У�����Ϊ��ȷ���� ��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵxOy�У�������![]() ��bΪ�������ĶԳ�����ֱ��x=1��
��bΪ�������ĶԳ�����ֱ��x=1��
��1����������ߵı���ʽ��
��2����A��8��m���ڸ��������ϣ������ڸ������߶Գ���ԳƵĵ�ΪA'�����A'�����ꣻ
��3��ѡȡ�ʵ������������±���������ͼ5��ʾ��ƽ��ֱ������ϵ����㣬�����������ߣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���![]() �ֱ���
�ֱ���![]() �ᡢ
�ᡢ![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() .����Ϊ
.����Ϊ![]() �������߾�����
�������߾�����![]() .
.
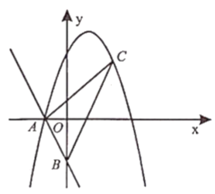
��1���������ߵĽ���ʽ��
��2����![]() Ϊ��һ������������һ����.���
Ϊ��һ������������һ����.���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() .��
.��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��ֵ�����
��ֵ�����![]() �����ֵ��
�����ֵ��
��3���ڣ�2���Ľ����£�����![]() ��
��![]() ���ϣ�
���ϣ�![]() Ϊֱ�������Σ���ֱ��д����
Ϊֱ�������Σ���ֱ��д����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
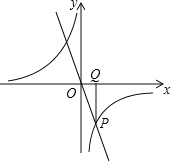
����Ŀ����֪����ͼ����P��һ��������������ͼ��������������y����2x��ͼ��Ĺ����㣬PQ��ֱ��x�ᣬ����Q������Ϊ��2��0����
��1������������������Ľ���ʽ��
��2�������M�����������������ͼ���ϣ�����MPQ�����Ϊ6�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�������ⷢ�֡�
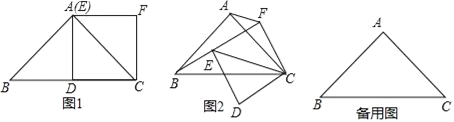
��ͼ1����Rt��ABC�У�AB=AC=2����BAC=90�㣬��DΪBC���е㣬��CDΪһ����������CDEF����Eǡ�����A�غϣ����߶�BE��AF��������ϵΪ�� ��
��2������չ�о���
�ڣ�1���������£����������CDEF�Ƶ�C��ת������BE��CE��AF���߶�BE��AF��������ϵ���ޱ仯�������ͼ2�����θ���֤����
��3�������ⷢ�֡�
��������CDEF��ת��B��E��F���㹲��ʱ��ֱ��д���߶�AF�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com