
【题目】如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
(1)判断AB与⊙O的位置关系,并说明理由;
(2)若PF:PC=1:2,AF=5,求CP的长.

【答案】(1))AB是⊙O切线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)结论:AB是⊙O切线,连接DE,CF,由∠FCD+∠CDF=90°,只要证明∠ADF=∠DCF即可解决问题.
(2)只要证明△PCF∽△PAC,得![]() ,设PF=a.则PC=2a,列出方程即可解决问题.
,设PF=a.则PC=2a,列出方程即可解决问题.
试题解析:(1)AB是⊙O切线.
理由:连接DE、CF.

∵CD是直径,
∴∠DEC=∠DFC=90°,
∵∠ACB=90°,
∴∠DEC+∠ACE=180°,
∴DE∥AC,
∴∠DEA=∠EAC=∠DCF,
∵∠DFC=90°,
∴∠FCD+∠CDF=90°,
∵∠ADF=∠EAC=∠DCF,
∴∠ADF+∠CDF=90°,
∴∠ADC=90°,
∴CD⊥AD,
∴AB是⊙O切线.
(2)∵∠CPF=∠CPA,∠PCF=∠PAC,
∴△PCF∽△PAC,
∴![]() ,
,
∴PC2=PFPA,设PF=a.则PC=2a,
∴4a2=a(a+5),
∴a=![]() ,
,
∴PC=2a=![]() .
.


科目:初中数学 来源: 题型:
【题目】某品牌专卖店对上个月销售的男运动鞋尺码统计如下:
码号(码) | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
销售量(双) | 6 | 8 | 14 | 20 | 17 | 3 | 1 |
这组统计数据中的众数是码.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB>AC,射线AM平分∠BAC.
(1)设AM交BC于点D,DE⊥AB于点E,DF⊥AC于点F,连接EF.有以下三种“判断”:
判断1:AD垂直平分EF.
判断2:EF垂直平分AD.
判断3:AD与EF互相垂直平分.
你同意哪个“判断”?简述理由;
(2)若射线AM上有一点N到△ABC的顶点B,C的距离相等,连接NB,NC.
①请指出△NBC的形状,并说明理由;
②当AB=11,AC=7时,求四边形ABNC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表为某市居民每月用水收费标准(单位:元/![]() ).
).
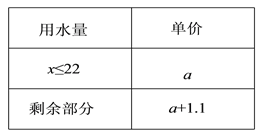
(1)某用户用水10立方米,共交水费23元,求a的值.
(2) 在(1)的前提下,该户5月份交水费71元,请问该用户用水多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.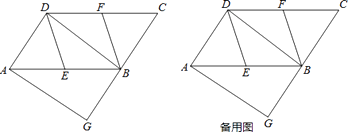
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形;
(3)请利用备用图分析,在(2)的条件下,若BE=4,∠DEB=120°,点M为BF的中点,当点P在BD边上运动时,求PF+PM的最小值,并求出此时线段BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
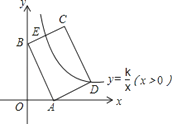
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=![]() (x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com