
【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①.AD=BC;②.DE=CF;③.BE∥AF.
⑴.请用其中两个关系式作为条件,另一个作为结论,写出所有正确的结论.
⑵.选择(1)中你写出的一个正确结论,说明它正确的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D,E分别是边AB,AC的中点,连接DE、BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH;
(2)若∠A=90°,求证:FG⊥FH;
(3)若∠A=80°,求∠GFH的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
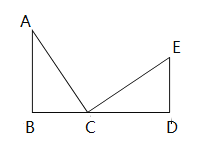
【题目】如图,在△ABC中,∠B=90°,点B、C、D在同一直线上,△ABC≌△CDE,且∠B=∠D,∠BAC=∠DCE.
(1)试说明BD=AB+ED;
(2)若∠CED=2∠BAC,求∠CED的度数;
(3)连接AE,则△ACE是怎样的三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=∠ACB,点D在BC边所在的直线上,点E在射线AC上,且始终保持∠ADE=∠AED.
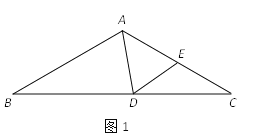
(1)如图1,若∠B=∠C=30°,∠BAD=70°,求∠CDE的度数;
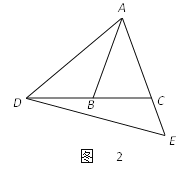
(2)如图2,若∠ABC=∠ACB=70°,∠CDE=15°,求∠BAD的度数;
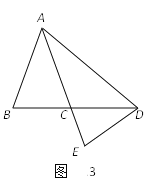
(3)如图3,当点D在BC边的延长线上时,猜想∠BAD与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论错误的是( )

A.BP=CM
B.△ABQ≌△CAP
C.∠CMQ的度数不变,始终等于60°
D.当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形
秒时,△PBQ为直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
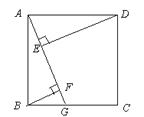
【题目】如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1) 求证:DE-BF = EF;
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com