练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，点P为等边△ABC的边AB上一点，点Q为BC延长线上一点，PA=CQ，连接PQ交AC于D，若CD=3，BQ=10，则PA的长为（　　）
    A．2B．2.2C．2.5D．2.4

    分析 利用平行线的性质结合相似三角形的判定与性质得出即可．

    解答 解：过点P作PF∥BC交AC于点F，如图1；
    ∵PF∥BC，
    ∴△APF∽△ABC，
    ∵△ABC是等边三角形，
    ∴△APF也是等边三角形，
    ∴∠APF=∠BCA=60°，AP=PF=AF=CQ，
    ∵CD=3，BQ=10，
    ∴2PA+6=10，
    ∴PA=2，
    故选A

    点评 本题考查了等边三角形的性质和判定，平行线的性质等知识点的应用，能综合运用性质进行推理是解此题的关键，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．已知某反比例函数的图象经过点（m，n），则它也一定经过（　　）
    A．（m，-n）B．（-n，-m）C．（-m，n）D．（-n，m）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．用配方法解方程x2-$\frac{2}{3}$x+1=0，正确的是（　　）
    A．（x-$\frac{2}{3}$）2=1，x1=$\frac{5}{3}$，x2=-$\frac{1}{3}$B．（x-$\frac{2}{3}$）2=$\frac{4}{9}$，x=$\frac{2±\sqrt{3}}{2}$
    C．（x-$\frac{2}{3}$）2=-$\frac{8}{9}$，原方程无实数解D．（x-$\frac{1}{3}$）2=-$\frac{8}{9}$，原方程无实数解

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．下列说法正确的是（　　）
    A．“任意画一个三角形，其内角和是360°”是随机事件
    B．“明天的降水概率为80%”，意味着明天降雨的可能性较大
    C．“某彩票中奖概率是1%”，表示买100张这种彩票一定会中奖
    D．晓芳抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为$\frac{7}{10}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．长沙市市政绿化工程中有一块面积为160m2的矩形空地，已知该矩形空地的长比宽多6m．
    （1）请算出该矩形空地的长与宽；
    （2）规划要求在矩形空地的中间留有两条互相垂直且宽度均为1m的人行甬道（其中两条人行甬道分别平行于矩形空地的长和宽），其余部分种上草．如果人行甬道的造价为260元/m2，种草区域的造价为220元/m2，那么这项工程的总造价为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．阅读理解
    （一）阅读与思考
    通过解方程（组）使问题得到解决的思维方式就是方程思想，刚学过的《勾股定理》及《一次函数》都与它有密切的联系．暑假后，方程家族也将迎来《一元二次方程》这一新成员，它的求解方法之一“配方法”，相信你一学就会，例如：解一元二次方程x2+2x-1=0
    解：x2+2x-1=0⇒x2+2x+1=2⇒（x+1）2=2⇒x+1=$\sqrt{2}$或x+1=-$\sqrt{2}$
    ∴x=-1+$\sqrt{2}$或x=-1-$\sqrt{2}$
    （二）解决问题
     如图1，矩形ABCD中，AB=9，AD=12，点G在CD上，且DG=5，点P从点B出发，以1单位每秒的速度在BC边上向点C运动，设点P的运动时间为x秒．
    （1）△APG的面积为y，求y关于x的函数关系式，并求y=34时x的值；
    （2）在点P从B向C运动的过程中，是否存在使AP⊥GP的时刻？若存在，求出x的值，若不存在，请说明理由；
    （3）如图2，M，N分别是AP、PG的中点，在点P从B向C运动的过程中，线段MN所扫过的图形是什么形状平行四边形，并直接写出它的面积15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．已知x+y=2，2y2-y-4=0，则y-$\frac{x}{y}$的值为$\frac{3}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．计算（-12）-（-3）+（-10）-（-9）-$\frac{1}{3}$的结果是（　　）
    A．$-\frac{25}{3}$B．$-\frac{43}{3}$C．$-\frac{49}{3}$D．$-\frac{31}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

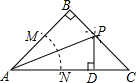    17．如图，在等腰直角△ABC中，B=90°，以点A为圆心任意长为半径画弧，与AB，AC分别交于点M，N，分别以点M，N为圆心大于$\frac{1}{2}$MN长为半径画弧，两弧交于点P，且点P刚好落在边BC上，AB=10cm，下列说法中：
    ①AB=AD；②AP平分∠BAC；③△PDC的周长是10$\sqrt{2}$cm；④AN=ND，
    正确的是（　　）
    A．①②③B．①②④C．①③④D．②③④

    查看答案和解析>>

    同步练习册答案