
已知x=1是一元二次方程x2+kx-2=0的一根,则方程的另一个根为 .
科目:初中数学 来源:2014-2015学年湖南省株洲市攸县七年级上学期期末测试数学试卷(解析版) 题型:选择题
A,B两地相距480 km,一列慢车从A地出发,每小时行驶60 km,一列快车从B地出发,每小时行驶90 km,快车提前30 min出发.两车相向而行,慢车行驶了多少小时后,两车相遇?若设慢车行驶了x h后,两车相遇,则根据题意,下面所列方程正确的是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:解答题
(1)观察发现
如图(1):若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
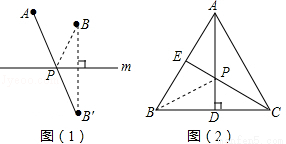
如图(2):在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 .
(2)实践运用
如图(3):已知⊙O的直径CD为2, 的度数为60°,点B是
的度数为60°,点B是 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,求BP+AP的最小值.
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,求BP+AP的最小值.
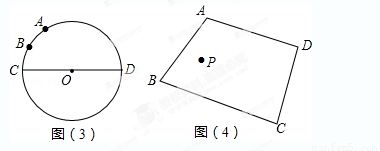
(3)拓展延伸
如图(4):点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使△PMN的周长最小,保留作图痕迹,不写作法.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:解答题
为了倡导“节约用水,从我做起”,宜兴市政府决定对市直机关500户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
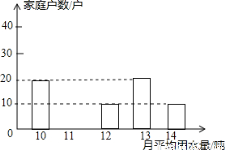
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计宜兴市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:选择题
如图,正方形ABCD的边长为9,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
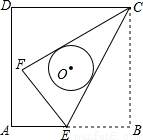
A.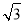 B.
B.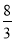
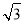 C.4
C.4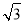 D.6
D.6
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:选择题
如图,在△ABC中,DE∥BC,若 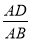 =
= 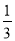 ,DE=2,则BC的值为 ( )
,DE=2,则BC的值为 ( )
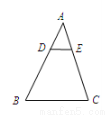
A.3 B.4 C.6 D.8
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:选择题
一元二次方程x2-8x+5=0的左边配成完全平方后所得的方程是( )
A.(x-6)2=11 B.(x-4)2=11
C.(x-4)2=21 D.以上答案都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com