
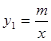 的图象与一次函数
的图象与一次函数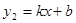 的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1.
的图象交于点M,N,已点M的坐标为(1,3),点N的纵坐标为-1.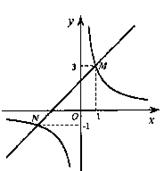
 ;此一次函数的解析式为:y=x+2.
;此一次函数的解析式为:y=x+2. ;
;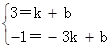 ,解得
,解得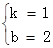 ,
,

科目:初中数学 来源:不详 题型:解答题
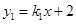 与反比例函数
与反比例函数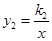 的图象交于点
的图象交于点 和
和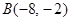 ,与
,与 轴交于点
轴交于点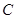 .(1)
.(1)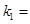 ,
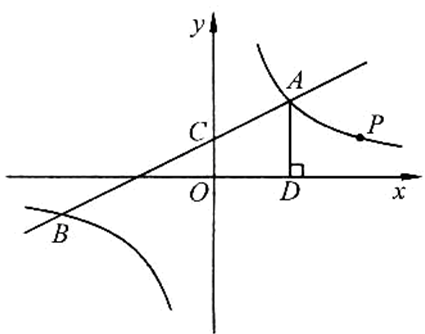
,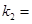 ;
;
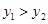 时,
时,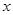 的取值范围是 ;
的取值范围是 ;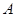 作
作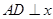 轴于点
轴于点 ,点
,点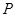 是反比例函数在第一象限的图象上一点,设直线
是反比例函数在第一象限的图象上一点,设直线 与线段
与线段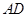 交于点
交于点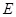 ,当
,当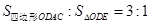 时,求点
时,求点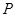 的坐标.
的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
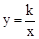 (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
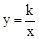 (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.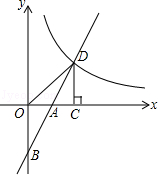
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 2,n)是反比例函数
2,n)是反比例函数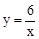 图像上的两个点,点C的坐标是(t,1),三角形ABC是直角三角形,则t的值是__________.
图像上的两个点,点C的坐标是(t,1),三角形ABC是直角三角形,则t的值是__________.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
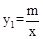 的图象经过点A,反比例函数
的图象经过点A,反比例函数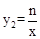 的图象经过点B,则下列关于m,n的关系正确的是
的图象经过点B,则下列关于m,n的关系正确的是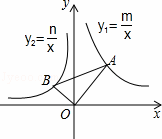
| A.m=﹣3n | B.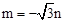 | C.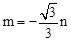 | D.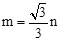 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com