
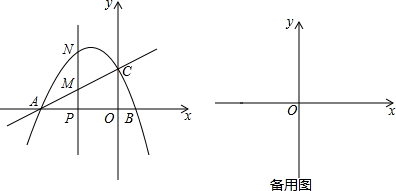
���� ��1���ѵ�C��0��2���������y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+c���������c���������䷽������������꣮
��2�������A��C���꣬��ֱ��AC����ʽΪy=kx+b����A��C�������ⷽ���鼴�ɣ�
��3������m��ʾ�߶�AP��PM������S=$\frac{1}{2}$•PA•PM���ɣ�
�ڷ����������з��̽�������P���߶�OA��ʱ����P���߶�OB��ʱ��
��� �⣺��1����������y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+c��y�ύ�ڵ�C��0��2����
��c=2��
�������߽���ʽΪy=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2=-$\frac{1}{2}$��x+$\frac{3}{2}$��2+$\frac{25}{8}$��
�������߶�������Ϊ��-$\frac{3}{2}$��$\frac{25}{8}$����
��2����y=0����-$\frac{1}{2}$x2-$\frac{3}{2}$x+2=0�����x=-4��1��
��A��-4��0����B��1��0����
��ֱ��AB����ʽΪy=kx+b������$\left\{\begin{array}{l}{-4k+b=0}\\{b=2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��AC����ʽΪy=$\frac{1}{2}$x+2��
��3������ͼ1�У�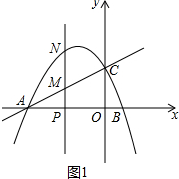
��P��m��0����PN��AB��
��M��m��$\frac{1}{2}$m+2����
��AP=4+m��PM=$\frac{1}{2}$m+2��
��S=$\frac{1}{2}$•PA•PM=$\frac{1}{2}$•��m+4����$\frac{1}{2}$m+2��=$\frac{1}{4}$m2+2m+4����-4��m��1����
����ͼ2�У�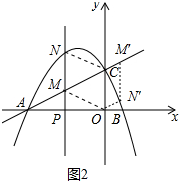
��MN��OC��N��m��-$\frac{1}{2}$m2-$\frac{3}{2}$m+2����
�൱MN=OCʱ���ı���MNCO��ƽ���ı��Σ�
����P���߶�OA��ʱ�У�-$\frac{1}{2}$m2-$\frac{3}{2}$m+2-��$\frac{1}{2}$m+2��=2�����m=-2��
��ʱS=$\frac{1}{4}$��4+4+4=10��
����P���߶�OB��ʱ�У���$\frac{1}{2}$m+2��-��-$\frac{1}{2}$m2-$\frac{3}{2}$m+2��=2�����m=-2+2$\sqrt{2}$��-2-2$\sqrt{2}$����������
��ʱS=3+2$\sqrt{2}$
����������S=10��3+2$\sqrt{2}$ʱ���Ե�M��N��C��OΪ������ı��λ��Ϊƽ���ı��Σ�
���� ���⿼����κ����ۺ��⡢һ�κ����������������ƽ���ı��ε��ж������ʵ�֪ʶ������Ĺؼ����������մ���ϵ����ȷ����������ʽ��ѧ�����ò���������⣬ѧ���÷��̵�˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
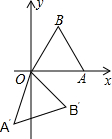 ��ͼ���ȱ�������OAB�Ķ���O������ԭ�㣬����A��x���ϣ�OA=2�����ȱ�������OAB��ԭ��˳ʱ����ת105����OA��B���λ�ã����B�������Ϊ��$\sqrt{2}$��-$\sqrt{2}$����
��ͼ���ȱ�������OAB�Ķ���O������ԭ�㣬����A��x���ϣ�OA=2�����ȱ�������OAB��ԭ��˳ʱ����ת105����OA��B���λ�ã����B�������Ϊ��$\sqrt{2}$��-$\sqrt{2}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
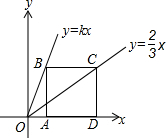 ��ͼ����B��C�ֱ�������ֱ��y=kx��y=$\frac{2}{3}$x�ϣ���A��D��x�������㣬��֪�ı���ABCD�������Σ���kֵΪ$\frac{2}{5}$��
��ͼ����B��C�ֱ�������ֱ��y=kx��y=$\frac{2}{3}$x�ϣ���A��D��x�������㣬��֪�ı���ABCD�������Σ���kֵΪ$\frac{2}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�CD��AE�ǡ�ABC�������ߣ�
��ͼ���ڡ�ABC�У�CD��AE�ǡ�ABC�������ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com