
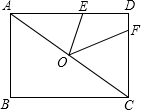
 如图,矩形ABCD中,点O为AC的中点,E,F分别在AD,CD上,且AE=AO,CF=CO.
如图,矩形ABCD中,点O为AC的中点,E,F分别在AD,CD上,且AE=AO,CF=CO.分析 解:(1)利用等腰三角形的性质得∠2=∠AEO,∠3=∠CFO,再根据三角形内角和定理得到∠1=180°-2∠2,∠4=180°-2∠3,则可计算出∠2+∠3=135°,然后利用平角的定义可计算出∠EOF=45°;
(2)利用平行四边形为中心对称图形,于是延长EO交BC于G,则△COG为所作;
(3)作FH⊥EG于H,连结GF,如图,易得△OFH为等腰直角三角形,所以FH=HO=$\frac{\sqrt{2}}{2}$OF=3$\sqrt{2}$,则利用中心对称的性质得OG=OE=4$\sqrt{2}$,CG=AE,接着根据勾股定理计算出GF=2$\sqrt{29}$,然后证明△CGF为等腰直角三角形得到CG=$\frac{\sqrt{2}}{2}$GF=$\sqrt{58}$,于是得到AC=2CG=2$\sqrt{58}$.
解答 解:(1)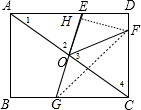 ∵AE=AO,CF=CO.
∵AE=AO,CF=CO.
∴∠2=∠AEO,∠3=∠CFO,
∴∠1=180°-2∠2,∠4=180°-2∠3,
而∠1+∠4=90°,
∴360°-2(∠2+∠3)=90°,
∴∠2+∠3=135°,
∴∠EOF=180°-(∠2+∠3)=45°;
(2)延长EO交BC于G,如图,则△COG为所作;
(3)作FH⊥EG于H,连结GF,如图,
∵∠EOF=45°,
∴△OFH为等腰直角三角形,
∴FH=HO=$\frac{\sqrt{2}}{2}$OF=$\frac{\sqrt{2}}{2}$×6=3$\sqrt{2}$,
∵△COG与△AOE关于点O成中心对称,
∴OG=OE=4$\sqrt{2}$,CG=AE,
∴GH=OG+OH=7$\sqrt{2}$,
在Rt△GFH中,GF=$\sqrt{G{H}^{2}+F{H}^{2}}$=$\sqrt{(7\sqrt{2})^{2}+(3\sqrt{2})^{2}}$=2$\sqrt{29}$,
∵点O为AC的中点,
∴CG=OC=CF,
∴△CGF为等腰直角三角形,
∴CG=$\frac{\sqrt{2}}{2}$GF=$\frac{\sqrt{2}}{2}$×2$\sqrt{29}$=$\sqrt{58}$,
∴AC=2CG=2$\sqrt{58}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.解决(3)小题的根据是利用45°构建等腰直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
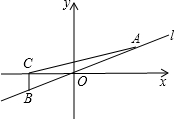 如图,点A(3,1)在直线l上.
如图,点A(3,1)在直线l上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com