
 ��ͼ����֪�Գ���Ϊx=-
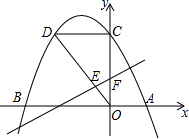
��ͼ����֪�Գ���Ϊx=- ��������y=ax2+bx+6��x�ύ��A��B���㣬��y�ύ��C�㣬OA=3��D����������һ�㣬��DC��OC��
��������y=ax2+bx+6��x�ύ��A��B���㣬��y�ύ��C�㣬OA=3��D����������һ�㣬��DC��OC�� x+m��OD���ڵ�E����y�ύ�ڵ�F����OE��DE=1��2����m��ֵ��
x+m��OD���ڵ�E����y�ύ�ڵ�F����OE��DE=1��2����m��ֵ�� ��������A��3��0����
��������A��3��0����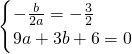 �����
����� ��
�� �������߽���ʽΪy=-
�������߽���ʽΪy=- x2-x+6��
x2-x+6�� x2-x+6��
x2-x+6�� x2-x+6=6��
x2-x+6=6��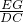 =
=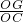 =
=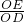 =
= ��
�� DC=1��OG=
DC=1��OG= OC=2��
OC=2�� x+m��
x+m�� +m��
+m�� ��
��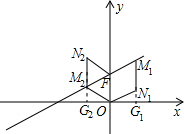 ��3����M��ֱ��EF��һ���㣬��x���Ϸ����ڵ�N��ʹ��O��F��M��NΪ������ı��������Σ�
��3����M��ֱ��EF��һ���㣬��x���Ϸ����ڵ�N��ʹ��O��F��M��NΪ������ı��������Σ� ��
�� x+
x+ �ϣ�
�ϣ� a+
a+ ����a��0�������N1��������a��
����a��0�������N1��������a�� a����
a���� a��2=��
a��2=�� ��2��
��2�� ��
�� ��
�� ����
���� ����a��0�������N2��������-2��4����
����a��0�������N2������Ϊ��-2��4����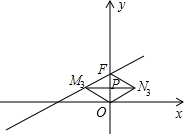 ����ͼ��OFΪ���εĶԽ���ʱ������M3N3����OF�ڵ�P����M3N3��OF���ഹֱƽ�֣�
����ͼ��OFΪ���εĶԽ���ʱ������M3N3����OF�ڵ�P����M3N3��OF���ഹֱƽ�֣� OF=
OF= ��
�� ʱ��
ʱ�� x+
x+ =
= ��
�� ��
�� ��
�� ����
���� ��
�� ����
���� ��
�� ����N2��-2��4����N3��
����N2��-2��4����N3�� ��
�� ����
���� x2-x+6��y�ύ��C������Ϊ��0��6������y=6���룬���x��ֵ���õ�D�����꼰DC=3���ٹ���E��EG��y���ڵ�G����EG��DC���õ���OEG�ס�ODC���������������ζ�Ӧ�߳ɱ����ó�
x2-x+6��y�ύ��C������Ϊ��0��6������y=6���룬���x��ֵ���õ�D�����꼰DC=3���ٹ���E��EG��y���ڵ�G����EG��DC���õ���OEG�ס�ODC���������������ζ�Ӧ�߳ɱ����ó�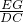 =
=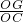 =
=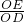 =
= �����EG��OG��ֵ���ó�E�����꣬Ȼ��E���������y=
�����EG��OG��ֵ���ó�E�����꣬Ȼ��E���������y= x+m���������m��ֵ��
x+m���������m��ֵ�� a+
a+ �������N1��������a��
�������N1������Ϊ��a�� a������Rt��OG1N1�У����ù��ɶ����ó�OG12+G1N12=ON12���г�����a�ķ��̣��ⷽ�̼��ɣ�ͬ�������N2�����ꣻ��OFΪ���εĶԽ���ʱ������M3N3����OF�ڵ�P���������ε����ʿ�֪M3N3��OF���ഹֱƽ�֣���OP=
a������Rt��OG1N1�У����ù��ɶ����ó�OG12+G1N12=ON12���г�����a�ķ��̣��ⷽ�̼��ɣ�ͬ�������N2�����ꣻ��OFΪ���εĶԽ���ʱ������M3N3����OF�ڵ�P���������ε����ʿ�֪M3N3��OF���ഹֱƽ�֣���OP= OF=
OF= ����y=
����y= ����y=
����y= x+
x+ �����x��ֵ�������õ���N3�����꣮
�����x��ֵ�������õ���N3�����꣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
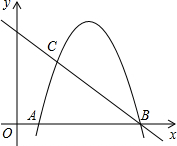 M��N��BΪ��������������ABC���ƣ�д��������̣�
M��N��BΪ��������������ABC���ƣ�д��������̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
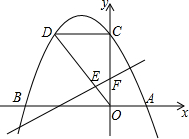 ��ͼ����֪�Գ���Ϊx=-
��ͼ����֪�Գ���Ϊx=-| 3 |
| 2 |
| 1 |
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012�����ʡ�Ƹ����ˮ�ػ�����ѧ�п���ѧģ���Ծ��������棩 ���ͣ������
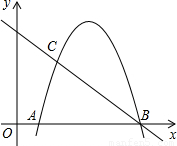
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�����ʡ�Ƹ���ѧ���Ƴ����п���ѧ��ģ�Ծ��������棩 ���ͣ������
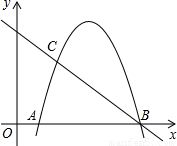
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com