
【题目】阅读下面材料,完成(1)~(3)题.
数学课上,老师出示了这样一道题:
如图1,△ABC中,AC=BC=a,∠ACB=90°,点D在AB上,且AD=kAB(其中0<k<![]() ),直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E,探究线段DC、DE的数量关系,并证明.
),直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E,探究线段DC、DE的数量关系,并证明.
同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现DC与DE相等”;
小伟:“通过构造全等三角形,经过进一步推理,可以得到DC与DE相等”
小强:“通过进一步的推理计算,可以得到BE与BC的数量关系”
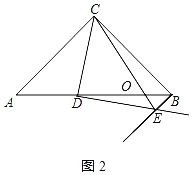
老师:“保留原题条件,连接CE交AB于点O.如果给出BO与DO的数量关系,那么可以求出COEO的值”
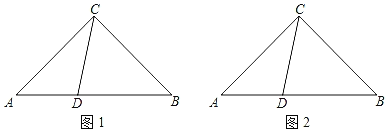
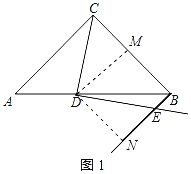
(1)在图1中将图补充完整,并证明DC=DE;
(2)直接写出线段BE与BC的数量关系 (用含k的代数式表示);
(3)在图2中将图补充完整,若BO=![]() DO,求COEO的值(用含a的代数式表示).
DO,求COEO的值(用含a的代数式表示).
【答案】(1)证明见解析;(2)BE=(1﹣2k)BC;(3)![]()
【解析】
(1)作DM⊥BC于M,DN作BE于N,则∠DMC=∠DNE=90°,由等腰直角三角形的性质得出∠ABC=45°,AB=![]() BC=
BC=![]() a,由旋转的性质得∠CDE=∠CBE=90°,则∠DBE=45°,∠MDN=90°,∠CDM=∠EDN,∠ABC=∠ABE,由角平分线的性质得出DM=DN,由ASA证得△CDM≌△EDN(ASA),即可得出结论;
a,由旋转的性质得∠CDE=∠CBE=90°,则∠DBE=45°,∠MDN=90°,∠CDM=∠EDN,∠ABC=∠ABE,由角平分线的性质得出DM=DN,由ASA证得△CDM≌△EDN(ASA),即可得出结论;
(2)由(1)得△CDM≌△EDN,则CM=EN,易证四边形BMDN是矩形,△BDM是等腰直角三角形,证明四边形BMDN是正方形,得出BM=BN,推出BC+BE=BM+CM+BM-CM=2BM=![]() BD,BD=AB-AD=(1-k)AB=(1-k)
BD,BD=AB-AD=(1-k)AB=(1-k)![]() BC,则BC+BE=
BC,则BC+BE=![]() BD=2(1-k)BC,即可得出结果;
BD=2(1-k)BC,即可得出结果;
(3)由∠CDE+∠CBE=90°+90°=180°,得出B、C、D、E四点共圆,得出COEO=DOBO,即可得出结果.
解:(1)将图补充完整,如图1所示:
作DM⊥BC于M,DN作BE于N,
则∠DMC=∠DNE=90°,
∵AC=BC=a,∠ACB=90°,
∴∠ABC=45°,AB=![]() BC=
BC=![]() ,
,
由旋转的性质得:∠CDE=∠CBE=90°,
∴∠DBE=90°﹣45°=45°,∠MDN=90°,
∴∠CDM=∠EDN,∠ABC=∠ABE,
∵DM⊥BC于M,DN作BE于N,
∴DM=DN,
在△CDM和△EDN中,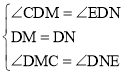 ,
,
∴△CDM≌△EDN(ASA),
∴DC=DE;
(2)BE=(1﹣2k)BC,理由如下:
由(1)得:△CDM≌△EDN,
∴CM=EN,
∵∠CBE=90°,DM⊥BC,DN⊥BE,
∴四边形BMDN是矩形,
∵∠ABC=45°,
∴△BDM是等腰直角三角形,
∴DM=BM,BM=![]() BD,
BD,
∴四边形BMDN是正方形,
∴BM=BN,
∵BC=BM+CM,
∴BC+BE=BM+CM+BM﹣CM=2BM=![]() BD,
BD,
∵AD=kAB,
∴BD=AB﹣AD=(1﹣k)AB=(1﹣k)![]() BC,
BC,
∴BC+BE=![]() BD=2(1﹣k)BC,
BD=2(1﹣k)BC,
整理得:BE=(1﹣2k)BC;
故答案为:BE=(1﹣2k)BC;
(3)将图补充完整,如图2所示:
∵∠CDE+∠CBE=90°+90°=180°,
∴B、C、D、E四点共圆,
∴COEO=DOBO,
∵BO=![]() DO,
DO,
∴COEO=DOBO=![]() DO2=
DO2=![]() ×(
×(![]() BD)2=
BD)2=![]() ×(
×(![]() )2×[(1﹣k)
)2×[(1﹣k)![]() a]2=
a]2=![]() .
.


科目:初中数学 来源: 题型:
【题目】小明利用灯光下自己的影子长度来测量路灯的高度.如图,CD和EF是两等高的路灯,相距27m,身高1.5m的小明(AB)站在两路灯之间(D、B、F共线),被两路灯同时照射留在地面的影长BQ=4m,BP=5m.
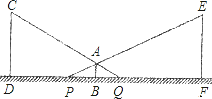
(1)小明距离路灯多远?
(2)求路灯高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形 ABCD 中,AD∥BC,∠ABC=90°,AB=BC,AE⊥BD,EF⊥CE
(1)试证明△AEF∽△BEC;
(2)如图,过 C 点作 CH⊥AD 于 H,试探究线段 DH 与 BF 的数量关系,并说明理由;
(3)若 AD=1,CD=5,试求出 BE 的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓东在解一元二次方程时,发现有这样一种解法:
如:解方程![]() .
.
解:原方程可变形,得
![]() .
.
![]() ,
,
![]() ,
,
![]()
直接开平方并整理,得![]() ,
,![]() .
.
我们称晓东这种解法为“平均数法”.
(1)下面是晓东用“平均数法”解方程![]() 时写的解题过程.
时写的解题过程.
![]() .
.
![]() ,
,
![]() .
.
直接开平方并整理,得![]() ,
,![]() .
.
上述过程中的“□”,“○”,“☆”,“¤”表示的数分别为________,________,________,________.
(2)请用“平均数法”解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 。
。
(1)抛物线的顶点坐标为_____________,点![]() 坐标为____________;(用含
坐标为____________;(用含![]() 的代数式表示);
的代数式表示);
(2)当![]() 时,抛物线上有一动点
时,抛物线上有一动点![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,且
,且![]() 。
。
①若点![]() 到
到![]() 轴的距离为2时,求点
轴的距离为2时,求点![]() 的坐标;
的坐标;
②设抛物线在点![]() 与点
与点![]() 之间部分(含点
之间部分(含点![]() 和点
和点![]() )最高点与最低点纵坐标之差为
)最高点与最低点纵坐标之差为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)若点![]() ,连结
,连结![]() ,当抛物线
,当抛物线![]() 与线段
与线段![]() 只有一个交点时,直接写出
只有一个交点时,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图l,四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一动点,连接
上一动点,连接![]() 并延长至点
并延长至点![]() ,使得
,使得![]() ,连接
,连接![]() 、
、![]() 、
、![]() 、
、![]() .
.
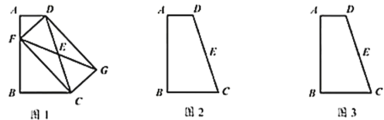
(1)四边形![]() 一定是___________(提醒你:填特殊四边形的名称);
一定是___________(提醒你:填特殊四边形的名称);
(2)如图2,若![]() ,
,![]() ,
,![]() ,是否存在这样的点
,是否存在这样的点![]() ,使得四边形
,使得四边形![]() 为菱形,若存在,计算菱形
为菱形,若存在,计算菱形![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
(3)如图3,若![]() ,
,![]() ,
,![]() (
(![]() ),是否存在这样的点
),是否存在这样的点![]() ,使得四边形
,使得四边形![]() 为矩形,若存在,请求出
为矩形,若存在,请求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
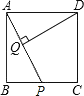
【题目】如图,在正方形ABCD中,AB=2,P是BC边上与B、C不重合的任意一点,DQ⊥AP于点Q
(1)判断△DAQ与△APB是否相似,并说明理由.
(2)当点P在BC上移动时,线段DQ也随之变化,设PA=x,DQ=y,求y与x间的函数关系式,并求出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com