
【题目】一张长为a宽为b的铁板(a>b),从四个角截去四个边长为x的小正方形 ![]() ,做成一个无盖的盒子,用代数式表示:
,做成一个无盖的盒子,用代数式表示:
(1)无盖盒子的外表面积;(用两种方法)
(2)无盖盒子的容积.
【答案】(1)ab-4x2或(a-2x)(b-2x)+2x(a-2x)+2x(b-2x)(有其它合理答案也对);(2) abx-2ax2-2bx2+4x3
【解析】(1)根据盒子的外表面积=5个面的面积之和或盒子的外表面积=长方形铁板的面积-4个小正方形的面积分别列出代数式即可.
(2)根据盒子的体积求法列出代数式即可=底面积×高.
(1)方法一:盒子的外表面积=5个面的面积之和,即为:(a-2x)(b-2x)+2×(a-2x)x+2×(b-2x)x=ab-4x2;
方法二:盒子的外表面积=长方形铁板的面积-4个小正方形的面积,即为:ab-4x2.
(2)无盖盒子的容积=(a-2x)(b-2x)x=abx-2ax2-2bx2+4x3.


科目:初中数学 来源: 题型:
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角板比较∠DOE与∠BOF的大小;
(3)借助量角器比较∠AOE与∠DOF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=﹣x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(﹣4,5),并与y轴交于点C,抛物线的对称轴为直线x=﹣1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=﹣1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=1,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N. 
(1)求证:AN=BD;
(2)填空:点P是⊙O上的一个动点, ①若AB=4,连结OC,则PC的最大值是;
②当∠BOP=时,以O,D,B,P为顶点四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在暑假社会实践活动中,以每千克![]() 元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了
元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了![]() 千克之后,余下的打折全部售完.销售金额
千克之后,余下的打折全部售完.销售金额![]() (元)售出西瓜的千克数
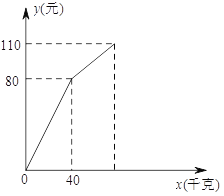
(元)售出西瓜的千克数![]() (千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:
(千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:
(![]() )求降价前销售金额
)求降价前销售金额![]() (元)与售出西瓜
(元)与售出西瓜![]() (千克)之间的关系;
(千克)之间的关系;
(![]() )小明这次社会实践活动赚了多少钱?
)小明这次社会实践活动赚了多少钱?
(![]() )若要使这次活动赚
)若要使这次活动赚![]() 元钱,问余下的西瓜应打几折销售完?
元钱,问余下的西瓜应打几折销售完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的,如果规定向东为正,行车里程(单位:km)如下:
+11, -2, +3, +9, -11, +5, -15, -8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为5元,成本为2.7元/km,则这天下午他盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com