
分析 令t=x2+2x-1,则原方程可化为at2+bt+c=0①,可得①有两个不相等的根t=$\frac{*b±\sqrt{{b}^{2}-4ac}}{2a}$,可得x2+2x-1=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$或x2+2x-1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,这两个方程有1个方程有两个相等的根,x2+2x-1-$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=0②或x2+2x-1-$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$=0③,分两种情况:方程②有两个相等的根x1,方程③有两个不相等的根x2,x3;方程③有两个相等的根,则方程2有两个不相等的根;进行讨论即可求解.
解答 解:令t=x2+2x-1,
则原方程可化为at2+bt+c=0①,
∴①有两个不相等的根t=$\frac{*b±\sqrt{{b}^{2}-4ac}}{2a}$,
∴x2+2x-1=$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$或x2+2x-1=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$,
这两个方程有1个方程有两个相等的根,
x2+2x-1-$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=0②或x2+2x-1-$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$=0③,
若方程②有两个相等的根x1,则方程③有两个不相等的根x2,x3,
x1=-$\frac{2}{2}$=-1,x2+x3=-$\frac{2}{1}$=-2,
x1+x2+x3=-3;
若方程③有两个相等的根,则方程2有两个不相等的根,
仍有x1+x2+x3=-3.
故答案为:-3.
点评 本题考查根的判别式,一元二次方程的解等知识,解题的关键是学会用转化的思想思考问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 18℃ | B. | 19℃ | C. | 20℃ | D. | 21℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
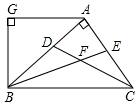 如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:
如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,下列结论:| A. | ①③④ | B. | ②④ | C. | ①③ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在一节“用频率估计概率”的复习课中,老师展示了一张折线统计图,它反映了某一结果出现的频率,则下列实验中最有可能符合这一结果的是( )
在一节“用频率估计概率”的复习课中,老师展示了一张折线统计图,它反映了某一结果出现的频率,则下列实验中最有可能符合这一结果的是( )| A. | 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀” | |
| B. | 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃 | |
| C. | 随机投掷一枚硬币,恰好正面朝上 | |
| D. | 掷一个质地均匀的正六面体骰子,向上的面点数是4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com