
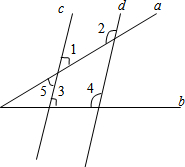
 直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.
直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°. 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:解答题
 已知:抛物线C1:y=x2-2x-3.
已知:抛物线C1:y=x2-2x-3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
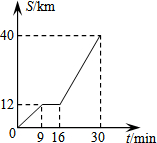 如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(km)与时间t(min)的函数关系图.观察图中所提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )
如图,将周长为8cm的△ABC沿BC方向平移1cm得到△DEF,则四边形ABFD周长为( )| A. | 8cm | B. | 10cm | C. | 12cm | D. | 16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com