
【题目】如图,抛物线y=-x2+bx+c与直线y=![]() x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,![]() ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.

(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
【答案】(1)y=-x2+![]() x+2.(2)1,2或
x+2.(2)1,2或![]() ;(3)(
;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)首先求出点C的坐标,然后利用待定系数法求出抛物线的解析式;
(2)本问采用数形结合的数学思想求解.将直线y=![]() x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;
x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;
(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标.
试题解析:(1)在直线解析式y=![]() x+2中,令x=0,得y=2,
x+2中,令x=0,得y=2,
∴C(0,2).
∵点C(0,2)、D(3,![]() )在抛物线y=-x2+bx+c上,
)在抛物线y=-x2+bx+c上,
∴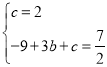 ,
,
解得b=![]() ,c=2,
,c=2,
∴抛物线的解析式为:y=-x2+![]() x+2.
x+2.
(2)∵PF∥OC,且以O、C、P、F为顶点的四边形是平行四边形,
∴PF=OC=2,
∴将直线y=![]() x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
由图1可以直观地看出,这样的交点有3个.

将直线y=![]() x+2沿y轴向上平移2个单位,得到直线y=
x+2沿y轴向上平移2个单位,得到直线y=![]() x+4,
x+4,
联立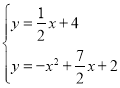 ,
,
解得x1=1,x2=2,
∴m1=1,m2=2;
将直线y=![]() x+2沿y轴向下平移2个单位,得到直线y=
x+2沿y轴向下平移2个单位,得到直线y=![]() x,
x,
联立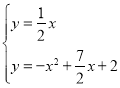 ,
,
解得x3=![]() ,x4=
,x4=![]() (在y轴左侧,不合题意,舍去),
(在y轴左侧,不合题意,舍去),
∴m3=![]() .
.
∴当m为值为1,2或![]() 时,以O、C、P、F为顶点的四边形是平行四边形.
时,以O、C、P、F为顶点的四边形是平行四边形.
(3)存在.
理由:设点P的横坐标为m,则P(m,-m2+![]() m+2),F(m,
m+2),F(m,![]() m+2).
m+2).
如图2所示,过点C作CM⊥PE于点M,则CM=m,EM=2,
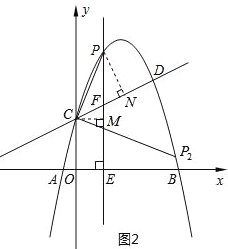
∴FM=yF-EM=![]() m,
m,
∴tan∠CFM=2.
在Rt△CFM中,由勾股定理得:CF=![]() m.
m.
过点P作PN⊥CD于点N,
则PN=FNtan∠PFN=FNtan∠CFM=2FN.
∵∠PCF=45°,
∴PN=CN,
而PN=2FN,
∴FN=CF=![]() m,PN=2FN=
m,PN=2FN=![]() m,
m,
在Rt△PFN中,由勾股定理得:PF=![]() m.
m.
∵PF=yP-yF=(-m2+![]() m+2)-(
m+2)-(![]() m+2)=-m2+3m,
m+2)=-m2+3m,
∴-m2+3m=![]() m,
m,
整理得:m2-![]() m=0,
m=0,
解得m=0(舍去)或m=![]() ,
,
∴P(![]() ,
,![]() );
);
同理求得,另一点为P(![]() ,
,![]() ).
).
∴符合条件的点P的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
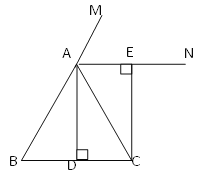
【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两队进行篮球比赛,规则规定:胜一场得3分,平一场得1分,负一场得0分.若两队共赛10场,甲队保持不败,且得分不低于22分,则甲队至少胜了场.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四种说法中正确的有( )
①过一点有且只有一条直线与已知直线垂直;②过直线外一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行;④过直线外一点,有且只有一条直线与已知直线平行。
A. 1种 B. 2种 C. 3种 D. 4种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别
从B、C两地同时出发,沿公路始终匀速相向而行,分别驶往C、B两地. 甲、乙两车与A地的距离y1、y2(千米)与行驶时间x(时)的关系如图2所示:
(1)请在图1中标出A地的位置,并写出相应的距离:AB= km,AC= km;
(2)在图2中求出甲车到达C地的时间a,并分别写出甲车到达A地之前y1与行驶时间x的关系式和甲车从A地离开到C地的y1与行驶时间x的关系式(不需要写自变量的取值范围);
(3)甲、乙两车都配有对讲机,对讲机在15千米之内(含15千米)时能够互相通话,请问两车能用对讲机通话的时间共有多长?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把地球看成一个表面光滑的球体,假设沿地球赤道绕紧一圈钢丝,然后把钢丝加长,使钢丝圈沿赤道处处高出球面16cm,那么钢丝大约需要加长
A. 102cm B. 104cm C. 106cm D. 108cm
查看答案和解析>>
科目:初中数学 来源: 题型:
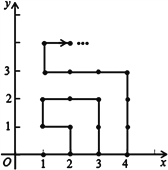
【题目】如图,在平面直接坐标系中,有若干个横坐标分别为整数的点,其顺序按图中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根据这个规律,则第2016个点的坐标为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com