
【题目】如图,在![]() 中,
中,![]() ,E为CA延长线上一点,D为AB上一点,F为
,E为CA延长线上一点,D为AB上一点,F为![]() 外一点且
外一点且![]() 连接DF,BF.
连接DF,BF.
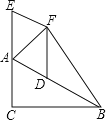
(1)当![]() 的度数是多少时,四边形ADFE为菱形,请说明理由:
的度数是多少时,四边形ADFE为菱形,请说明理由:
(2)当AB= 时,四边形ACBF为正方形(请直接写出)
【答案】(1)当![]() 时,四边形ADFE为菱形,理由详见解析; (2)
时,四边形ADFE为菱形,理由详见解析; (2)![]() .
.
【解析】
(1)当∠CAB=60°时,四边形ADFE为菱形;由平行线的性质可证∠AFE=∠DAF,∠AEF=∠CAB=60°,可得△AEF,△AFD都是等边三角形,可得AE=AF=AD=EF=FD,即可得结论.
(2)由正方形的性质可求解.
(1)当∠CAB=60°时,四边形ADFE为菱形,
理由如下:
∵AE=AF=AD
∴∠AEF=∠AFE,
∵EF∥AB
∴∠AFE=∠DAF,∠AEF=∠CAB=60°
∴∠FAD=60°
∴△AEF,△AFD都是等边三角形
∴AE=AF=AD=EF=FD
∴四边形ADFE为菱形
(2)若四边形ACBF为正方形
∴AC=BC=1,∠ACB=90°
∴AB=![]()
∴当AB=![]() 时,四边形ACBF为正方形
时,四边形ACBF为正方形
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC的中点,DE⊥BC交AC于点E,已知AD=AB,连接BE交AD于点F,下列结论:①BE=CE;②∠CAD=∠ABE;③S△ABF=3S△DEF;④△DEF∽△DAE,其中正确的有( )
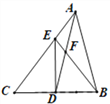
A. 1个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据第五次、第六次全国人口普查结果显示:某市常住人口总数由第五次的400万人增加到第六次的450万人,常住人口的学历状况统计图如图所示(部分信息未给出):

解答下列问题:
(1)求第六次人口普查小学学历的人数,并把条形统计图补充完整;
(2)求第五次人口普查中该市常住人口每万人中具有初中学历的人数;
(3)第六次人口普查结果与第五次相比,每万人中初中学历的人数增加了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
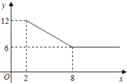
【题目】某公司经营杨梅业务,以3万元/吨的价格买入杨梅后,分拣成A、B两类,A类杨梅包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(万元/吨)与销售数量x(x≥2,单位:吨)之间的函数关系如图;B类杨梅深加工后再销售,深加工总费用s(万元)与加工数量t(吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)A类杨梅的销售量为5吨时,它的平均销售价格是每吨多少万元?
(2)若该公司收购10吨杨梅,其中A类杨梅有4吨,则经营这批杨梅所获得的毛利润(w)为多少万元?(毛利润=销售总收入﹣经营总成本)
(3)若该公司收购20吨杨梅,要使该公司获得30万元毛利润,求直销的A类杨梅有多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOC=∠BOD=120°,∠BOC=![]() ∠AOD.
∠AOD.
(1)求∠AOD的度数;
(2)若射线OB绕点O以每秒旋转20°的速度顺时针旋转,同时射线OC以每秒旋转15°的速度逆时针旋转,设旋转的时间为t秒(0<t<6),试求当∠BOC=20°时t的值;
(3)若∠AOB绕点O以每秒旋转5°的速度逆时针旋转,同时∠COD绕点O以每秒旋转10°的速度逆时针旋转,设旋转的时间为t秒(0<t<18),OM平分∠AOC,ON平分∠BOD,在旋转的过程中,∠MON的度数是否发生改变?若不变,求出其值:若改变,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
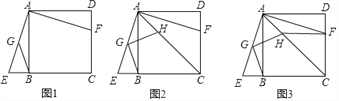
【题目】已知:如图1.正方形ABCD,过点A作∠EAF=90°,两边分别交直线BC于点E,交线段CD于点F,G为AE中点,连接BG
(1)求证:△ABE≌△ADF
(2)如图2,过点G作BG的垂线交对角线AC于点H,求证:GH=GB;
(3)如图3,连接HF,若CH=3AH,AD=2![]() ,求线段HF的长.
,求线段HF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
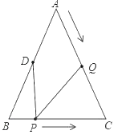
【题目】如图,已知△ABC中,AB=AC=12cm,BC=10cm,点D为AB的中点,如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C 以4cm/s的速度运动.若点P、Q两点分别从点B、A同时出发.
(1)经过2秒后,求证:∠DPQ=∠C.
(2)若△CPQ的周长为18cm,问经过几秒钟后,△CPQ是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a,宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为_________;小正方形(阴影部分)的边长为_________.(用含a,b的代数式表示)
(2)仔细观察图,请你写出下列三个代数式(a+b)2,(a-b)2,ab所表示的图形面积之间的相等关系.
(3)已知a+b=7,ab=6,求代数式(a-b)2的值.
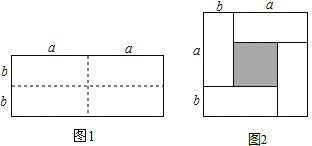
查看答案和解析>>
科目:初中数学 来源: 题型:
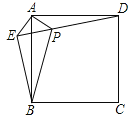
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )
A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com