
【题目】综合与实践
折纸是同学们喜欢的手工活动之一,通过折纸我们既可以得到许多美丽的图形,同时折纸的过程还蕴含着丰富的数学知识.
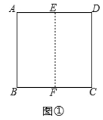
折一折:把边长为4的正方形纸片![]() 对折,使边
对折,使边![]() 与
与![]() 重合,展开后得到折痕
重合,展开后得到折痕![]() .如图①:
.如图①:![]() 为
为![]() 上一点,将正方形纸片
上一点,将正方形纸片![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 的点
的点![]() 处,展开后连接
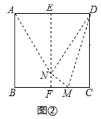
处,展开后连接![]() ,如图②
,如图②
(一)做一做:
(1)图②中,求![]() 的度数和线段
的度数和线段![]() 的长度.
的长度.
(2)图②中,试判断![]() 的形状,并给出证明.
的形状,并给出证明.
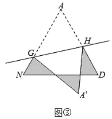
剪一剪、折一折:将图②中的![]() 剪下来,将其沿直线
剪下来,将其沿直线![]() 折叠,使点
折叠,使点![]() 落在点
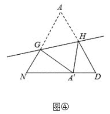
落在点![]() 处,分别得到图③、图④.
处,分别得到图③、图④.
(二)填一填:
(3)图③中阴影部分的周长为________.
(4)图③中,若![]() ,则
,则![]() __________
__________![]() .
.
(5)如图④点![]() 落在边
落在边![]() 上,若
上,若![]() ,则
,则![]() ______(用含
______(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 是等边三角形,理由详见解析;(3)12;(4)
是等边三角形,理由详见解析;(3)12;(4)![]() ;(5)
;(5)![]()
【解析】
(1)由折叠得四边形CDEF是矩形,ED=![]() AD=2,DN=CD=4,求出∠CDN=∠END=30°,
AD=2,DN=CD=4,求出∠CDN=∠END=30°,
由折叠得∠CDM=∠NDM得到∠CDM=15°,根据∠CMD=90°-∠CDM求出度数,根据EN=![]() ,EF=CD=4,求出NF=
,EF=CD=4,求出NF=![]() ;
;
(2)![]() 是等边三角形;由折叠得AE=DE,∠AEN=∠DEN=90°,证得
是等边三角形;由折叠得AE=DE,∠AEN=∠DEN=90°,证得![]() ,得到
,得到![]() ,再求出∠AND=90°-∠CDN=60°,即可得到△AND是等边三角形;
,再求出∠AND=90°-∠CDN=60°,即可得到△AND是等边三角形;
(3)根据等边三角形的性质得到AN=ND=AD=4,阴影部分的周长=NG+![]() +
+![]() +DH+ND=AN+AD+ND即可求出答案;
+DH+ND=AN+AD+ND即可求出答案;
(4)由![]() ,求出
,求出![]() ,利用四边形的内角和360°求出
,利用四边形的内角和360°求出![]() 再根据邻补角求出答案;
再根据邻补角求出答案;
(5)根据![]() 设
设![]() ,
,![]() (b>0),得到AN=ND=AD=b(m+n),证明△
(b>0),得到AN=ND=AD=b(m+n),证明△![]() ∽△
∽△![]() ,得到
,得到![]() =
=![]() ,即可求出答案.
,即可求出答案.
(1)由折叠得四边形CDEF是矩形,ED=![]() AD=2,DN=CD=4,
AD=2,DN=CD=4,
∵∠DEF=90°,ED=![]() DN,
DN,
∴∠END=30°,
∴∠CDN=∠END=30°,
由折叠得∠CDM=∠NDM,
∴∠CDM=15°,
∴∠CMD=90°-∠CDM=75°,
∵EN=![]() ,EF=CD=4,
,EF=CD=4,
∴NF=![]() ;
;
(2)![]() 是等边三角形;
是等边三角形;
证明:由折叠得AE=DE,∠AEN=∠DEN=90°,
又∵EN=EN,
∴![]() ,
,
∴![]() ,
,
∵∠AND=90°-∠CDN=60°,
∴△AND是等边三角形;
(3)∵△AND是等边三角形,
∴AN=ND=AD=4,
∴阴影部分的周长=NG+![]() +
+![]() +DH+ND=AN+AD+ND=12,
+DH+ND=AN+AD+ND=12,
故答案为:12;
(4)∵![]() ,
,
∴![]() ,
,
∵∠A=![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(5)∵![]() ,
,
∴设![]() ,
,![]() (b>0),
(b>0),
∵△AND是等边三角形,
∴AN=ND=AD=b(m+n),
∵![]() ,
,
∴![]() ,
,
∵∠N=∠D=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴△![]() ∽△
∽△![]() ,
,
∴![]() ,
,
=![]() .
.
∴![]()
![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点 A 在反比例函数![]() (x>0)的图象上,则经过点 B 的反比例函数解式为_________.
(x>0)的图象上,则经过点 B 的反比例函数解式为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD与正方形CEFG,M是AF的中点,连接DM,EM.
(1)如图1,点E在CD上,点G在BC的延长线上,请判断DM,EM的数量关系与位置关系,并直接写出结论;
(2)如图2,点E在DC的延长线上,点G在BC上,(1)中结论是否仍然成立?请证明你的结论;
(3)将图1中的正方形CEFG绕点C旋转,使D,E,F三点在一条直线上,若AB=13,CE=5,请画出图形,并直接写出MF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得![]() ,即
,即![]() ;由周长为m,得
;由周长为m,得![]() ,即
,即![]() .满足要求的
.满足要求的![]() 应是两个函数图象在第 象限内交点的坐标.
应是两个函数图象在第 象限内交点的坐标.
(2)画出函数图象
函数![]() 的图象如图所示,而函数
的图象如图所示,而函数![]() 的图象可由直线
的图象可由直线![]() 平移得到.请在同一直角坐标系中直接画出直线
平移得到.请在同一直角坐标系中直接画出直线![]() .
.
(3)平移直线![]() ,观察函数图象
,观察函数图象
①当直线平移到与函数![]() 的图象有唯一交点
的图象有唯一交点![]() 时,周长m的值为 ;
时,周长m的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
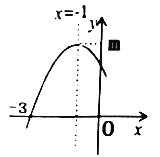
【题目】二次函数![]() 图象的一部分如图所示,顶点坐标为
图象的一部分如图所示,顶点坐标为![]() ,与
,与![]() 轴的一个交点的坐标为(-3,0),给出以下结论:①
轴的一个交点的坐标为(-3,0),给出以下结论:①![]() ;②
;②![]() ;③若
;③若![]() 、
、![]() 为函数图象上的两点,则
为函数图象上的两点,则![]() ;④当
;④当![]() 时方程
时方程![]() 有实数根,则
有实数根,则![]() 的取值范围是
的取值范围是![]() .其中正确的结论的个数为( )
.其中正确的结论的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是![]()
![]()

A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() (
(![]() 是常数,
是常数,![]() )与直线
)与直线![]() 都经过
都经过![]() 轴上的一点
轴上的一点![]() ,且抛物线
,且抛物线![]() 的顶点
的顶点![]() 在直线
在直线![]() 上,则称此直线
上,则称此直线![]() 与该抛物线
与该抛物线![]() 具有“一带一路”关系.此时,直线
具有“一带一路”关系.此时,直线![]() 叫做抛物线
叫做抛物线![]() 的“带线”,抛物线
的“带线”,抛物线![]() 叫做直线
叫做直线![]() 的“路线”.
的“路线”.
(1)若直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,求
具有“一带一路”关系,求![]() 的值;
的值;
(2)若某“路线”![]() 的顶点在反比例函数
的顶点在反比例函数![]() 的图象上,它的“带线”
的图象上,它的“带线”![]() 的解析式为
的解析式为![]() ,求此“路线”
,求此“路线”![]() 的解析式;
的解析式;
(3)当常数![]() 满足
满足![]() 时,请直接写出抛物线
时,请直接写出抛物线![]() :
:![]() 的“带线”
的“带线”![]() 与
与![]() 轴,
轴,![]() 轴所围成的三角形面积S的取值范围.
轴所围成的三角形面积S的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com