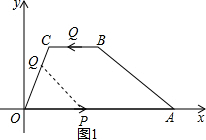
ЗжЮіЃКЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіЖўДЮКЏЪ§НтЮіЪНМДПЩЃЛ
ЃЈ2ЃЉИљОнвбжЊЕУГіЁїOPQЕФИпЃЌНјЖјРћгУШ§НЧаЮУцЛ§ЙЋЪНЧѓГіМДПЩЃЛ
ЃЈ3ЃЉИљОнЬтвтЕУГіЃК0ЁмtЁм3ЃЌЕБ0ЁмtЁм2ЪБЃЌQдкBCБпЩЯдЫЖЏЃЌЕУГіШєЁїOPQЮЊжБНЧШ§НЧаЮЃЌжЛФмЪЧЁЯOPQ=90ЁуЛђЁЯOQP=90ЁуЃЌЕБ2ЃМtЁм3ЪБЃЌQдкOCБпЩЯдЫЖЏЃЌЕУГіЁїOPQВЛПЩФмЮЊжБНЧШ§НЧаЮЃЛ
ЃЈ4ЃЉЪзЯШЧѓГіХзЮяЯпЖдГЦжсвдМАOBжБЯпНтЮіЪНКЭPMЕФНтЮіЪНЃЌЕУГі
ЃЈ1-tЃЉЁС
=3-t-2tЃЌКуГЩСЂЃЌМД0ЁмtЁм2ЪБЃЌPЃЌMЃЌQзмдквЛЬѕжБЯпЩЯЃЌдйРћгУ2ЃМtЁм3ЪБЃЌЧѓГіtЕФжЕЃЌИљОнtЕФШЁжЕЗЖЮЇЕУГіД№АИЃЎ
НтД№ЃКНтЃКЃЈ1ЃЉЩшЫљЧѓХзЮяЯпЕФНтЮіЪНЮЊy=ax
2+bx+cЃЌАбAЃЈ6ЃЌ0ЃЉЃЌBЃЈ3ЃЌ
ЃЉЃЌCЃЈ1ЃЌ
ЃЉШ§ЕузјБъДњШыЕУЃК
ЃЌ
НтЕУЃК
ЃЌ
МДЫљЧѓХзЮяЯпНтЮіЪНЮЊЃКy=-
x
2+
x+
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌвРОнЬтвтЕУГіЃКOC=CB=2ЃЌЁЯCOA=60ЁуЃЌ
ЁрЕБЖЏЕуQдЫЖЏЕНOCБпЪБЃЌOQ=4-tЃЌ
ЁрЁїOPQЕФИпЮЊЃКOQЁСsin60Ёу=ЃЈ4-tЃЉЁС
ЃЌ
гжЁпOP=2tЃЌ
ЁрS=
ЁС2tЁСЃЈ4-tЃЉЁС
=-
ЃЈt
2-4tЃЉЃЈ2ЁмtЁм3ЃЉЃЛ
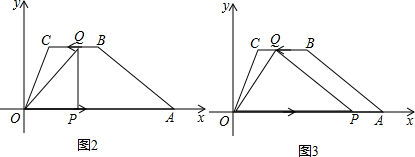
ЃЈ3ЃЉИљОнЬтвтЕУГіЃК0ЁмtЁм3ЃЌ
ЕБ0ЁмtЁм2ЪБЃЌQдкBCБпЩЯдЫЖЏЃЌДЫЪБOP=2tЃЌOQ=
ЃЌ
PQ=
=
ЃЌ
ЁпЁЯPOQЃМЁЯPOC=60ЁуЃЌ
ЁрШєЁїOPQЮЊжБНЧШ§НЧаЮЃЌжЛФмЪЧЁЯOPQ=90ЁуЛђЁЯOQP=90ЁуЃЌ
ШєЁЯOPQ=90ЁуЃЌШчЭМ2ЃЌдђOP
2+PQ
2=QO
2ЃЌМД4t
2+3+ЃЈ3t-3ЃЉ
2=3+ЃЈ3-tЃЉ
2ЃЌ
НтЕУЃКt
1=1ЃЌt
2=0ЃЈЩсШЅЃЉЃЌ
ШєЁїOPQЮЊжБНЧШ§НЧаЮЃЌжЛФмЪЧЁЯOPQ=90ЁуЛђЁЯOQP=90ЁуЃЌ
ШєЁЯOQP=90ЁуЃЌШчЭМЃЌ3ЃЌдђOQ
2+PQ
2=PO
2ЃЌМДЃЈ3-tЃЉ
2+6+ЃЈ3t-3ЃЉ
2=4t
2ЃЌ
НтЕУЃКt=2ЃЌ
ЕБ2ЃМtЁм3ЪБЃЌQдкOCБпЩЯдЫЖЏЃЌДЫЪБOP=2tЃО4ЃЌ
ЁЯPOQ=ЁЯCOP=60ЁуЃЌ
OQЃМOC=2ЃЌ
ЙЪЁїOPQВЛПЩФмЮЊжБНЧШ§НЧаЮЃЌ
злЩЯЫљЪіЃЌЕБt=1Лђt=2ЪБЃЌЁїOPQЮЊжБНЧШ§НЧаЮЃЛ
ЃЈ4ЃЉгЩЃЈ1ЃЉПЩжЊЃЌХзЮяЯпy=-
x
2+
x+
=-
ЃЈx-2ЃЉ
2+
ЃЌ
ЦфЖдГЦжсЮЊx=2ЃЌ
гжЁпOBЕФжБЯпЗНГЬЮЊy=
xЃЌ
ЁрХзЮяЯпЖдГЦжсгыOBНЛЕуЮЊMЃЈ2ЃЌ
ЃЉЃЌ
гжЁпPЃЈ2tЃЌ0ЃЉ
ЩшЙ§PЃЌMЕФжБЯпНтЮіЪНЮЊЃКy=kx+bЃЌ
Ёр
ЃЌ
НтЕУЃК
ЃЌ
МДжБЯпPMЕФНтЮіЪНЮЊЃКy=
x-
ЃЌ
МД
ЃЈ1-tЃЉy=x-2tЃЌ
гж0ЁмtЁм2ЪБЃЌQЃЈ3-tЃЌ
ЃЉЃЌДњШыЩЯЪНЃЌЕУЃК
ЃЈ1-tЃЉЁС
=3-t-2tЃЌКуГЩСЂЃЌ
МД0ЁмtЁм2ЪБЃЌPЃЌMЃЌQзмдквЛЬѕжБЯпЩЯЃЌ
МДMдкжБЯпPQЩЯЃЛ
ЕБ2ЃМtЁм3ЪБЃЌOQ=4-tЃЌЁЯQOP=60ЁуЃЌ
ЁрQЃЈ
ЃЌ
ЃЉЃЌ
ДњШыЩЯЪНЕУЃК
ЁС
ЃЈ1-tЃЉ=
-2tЃЌ
НтЕУЃКt=2Лђt=
ЃЈОљВЛКЯЬтвтЃЌЩсШЅЃЉЃЎ
ЁрзлЩЯЫљЪіЃЌПЩжЊЙ§ЕуAЁЂBЁЂCШ§ЕуЕФХзЮяЯпЕФЖдГЦжсOBКЭPQФмЙЛНЛгквЛЕуЃЌДЫЪБ0ЁмtЁм2ЃЎ

 ЃЈ2013•ЛЦИдЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮABCDЪЧЬнаЮЃЌЦфжаAЃЈ6ЃЌ0ЃЉЃЌBЃЈ3ЃЌ
ЃЈ2013•ЛЦИдЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮABCDЪЧЬнаЮЃЌЦфжаAЃЈ6ЃЌ0ЃЉЃЌBЃЈ3ЃЌ



 53ЫцЬУВтЯЕСаД№АИ
53ЫцЬУВтЯЕСаД№АИ

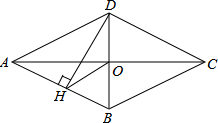 ЃЈ2013•ЛЦИдЃЉШчЭМЃЌЫФБпаЮABCDЪЧСтаЮЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌDHЁЭABгкHЃЌСЌНгOHЃЌЧѓжЄЃКЁЯDHO=ЁЯDCOЃЎ
ЃЈ2013•ЛЦИдЃЉШчЭМЃЌЫФБпаЮABCDЪЧСтаЮЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌDHЁЭABгкHЃЌСЌНгOHЃЌЧѓжЄЃКЁЯDHO=ЁЯDCOЃЎ
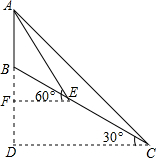 ЃЈ2013•ЛЦИдЃЉШчЭМЃЌаЁЩНЖЅЩЯгавЛаХКХЫўABЃЌЩНЦТBCЕФЧуНЧЮЊ30ЁуЃЌЯжЮЊСЫВтСПЫўИпABЃЌВтСПШЫдБбЁдёЩННХCДІЮЊвЛВтСПЕуЃЌВтЕУЫўЖЅбіНЧЮЊ45ЁуЃЌШЛКѓЫГЩНЦТЯђЩЯаазп100УзЕНДяEДІЃЌдйВтЕУЫўЖЅбіНЧЮЊ60ЁуЃЌЧѓЫўИпABЃЈНсЙћБЃСєећЪ§ЃЌ
ЃЈ2013•ЛЦИдЃЉШчЭМЃЌаЁЩНЖЅЩЯгавЛаХКХЫўABЃЌЩНЦТBCЕФЧуНЧЮЊ30ЁуЃЌЯжЮЊСЫВтСПЫўИпABЃЌВтСПШЫдБбЁдёЩННХCДІЮЊвЛВтСПЕуЃЌВтЕУЫўЖЅбіНЧЮЊ45ЁуЃЌШЛКѓЫГЩНЦТЯђЩЯаазп100УзЕНДяEДІЃЌдйВтЕУЫўЖЅбіНЧЮЊ60ЁуЃЌЧѓЫўИпABЃЈНсЙћБЃСєећЪ§ЃЌ