
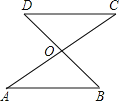
【题目】如图,线段AC与BD交于点D,且OA =OC,请添加一个条件,使△OA B≌△OCD,这个条件是___________.
【答案】∠A=∠C,∠B=∠D,OD=OB,AB∥CD.
【解析】本题要判定△OAB≌△OCD,已知OA=OC,∠AOB=∠COD,具备了一组边对应相等和一组角对应相等,故添加∠A=∠C,∠B=∠D,OD=OB,AB∥CD后可分别根据ASA、AAS、SAS、AAS判定△OAB≌△OCD.
解:∵OA=OC,∠A=∠C,∠AOB=∠COD,
∴△OAB≌△OCD(ASA).
∵OA=OC,∠B=∠D,∠AOB=∠COD,
∴△OAB≌△OCD(AAS).
∵OA=OC,OD=OB,∠AOB=∠COD,
∴△OAB≌△OCD(SAS).
∵AB∥CD,
∴∠A=∠C,∠B=∠D(两直线平行,内错角相等),
∵OA=OC,
∴△OAB≌△OCD(AAS).
故填∠A=∠C,∠B=∠D,OD=OB,AB∥CD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在世界环境日到来之际,希望中学开展了“环境与人类生存”主题研讨活动,活动之一是对我们的生存环境进行社会调查,并对学生的调查报告进行评比.初三.(3)班将本班50篇学生调查报告得分进行整理(成绩均为整数),列出了频率分布表,并画出了频率分布直方图(部分)如下:
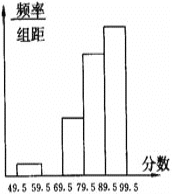
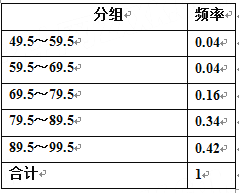
根据以上信息回答下列问题:
(1)该班90分以上(含90分)的调查报告共有________篇;
(2)该班被评为优秀等级(80分及80分以上)的调查报告占_________%;
(3)补全频率分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广东省梅州市第23题)(为方便答题,可在答题卡上画出你认为必要的图形)
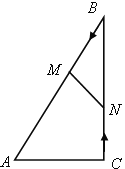
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB 边上以每秒![]() cm的速度向点B匀速运动,设运动时间为t秒(0
cm的速度向点B匀速运动,设运动时间为t秒(0![]() ),连接MN.
),连接MN.
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b为有理数,有下列结论正确的是( )
A. 如果a>b,那么|a|>|b| B. 如果|a|≠|b|,那么a≠b
C. 如果a>b, 那么a2>b2 D. 如果a2>b2,那么a>b
查看答案和解析>>
科目:初中数学 来源: 题型:
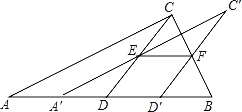
【题目】(2016湖北省荆州市第21题)如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com