
【题目】如图,在矩形ABCD(AD>AB)中,P为BC边上的一点,AP=AD,过点P作PE⊥PA交CD于E,连接AE并延长交BC的延长线于F.
(1)求证:△APE≌△ADE;
(2)若AB=3,CP=1,试求BP,CF的长;
(3)在(2)的条件下,连结PD,若点M为AP上的动点,N为AD延长线上的动点,且PM=DN,连结MN交PD于G,作MH⊥PD,垂足为H,试问当M、N在移动过程中,线段GH的长度是否发生变化?若变化,请说明理由,若不变,求出GH的长.

【答案】(1)详见解析;(2)BP=4,CF=4;(3)没有变化,GH=![]() .
.
【解析】
(1)先判断出∠APE=∠D=90°,即可得出结论;
(2)先求出CD=AB=3,进而利用勾股定理求出CE=![]() ,DE=
,DE=![]() ,再△ABP∽△PCE,即可得出BP=4即可得出结论;
,再△ABP∽△PCE,即可得出BP=4即可得出结论;
(3)先判断出MI=DN,进而判断出△MGH≌△NGD,最后用勾股定理即可得出结论.
(1)证明:
∵在矩形ABCD中,∠D=90°,又PE⊥PA,
∴∠APE=∠D=90°,
又∵AP=AD,AE=AE,
∴△APE≌△ADE
(2)由△APE≌△ADE得DE=PE
∵AB=3,
∴CD=AB=3
∴在Rt△PCE中,设CE=x,则PE=3﹣x,
∴(3﹣x)2=x2+12,解得x=![]()
∴CE=![]() ,DE=
,DE=![]()
又∵∠B=∠BCD=∠APE=90°
∴∠PEC+∠CPE=90°,∠APB+∠CPE=90°
∴∠PEC=∠APB
∴△ABP∽△PCE
∴![]() ,得BP=4
,得BP=4
∴在Rt△ABP中,AP=AD=5,
又∵AD∥BC
∴ ![]() ,
,
∴CF=4
(3)没有变化H
如图2,
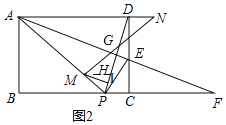
作MI∥DN交PD于I
∵AD=AP,MI∥DN
∴∠ADP=∠APD,∠ADP=∠MIP
∴∠APD=∠MIP
∴MI=PM
又∵MH⊥PD
∴PH=HI
又∵PM=DN
∴MI=DN
∴∠MGI=∠DGN,∠IMG=∠DNG,
∴△MGH≌△NGD
∴GI=GD
∴GH=GI+IH=![]() PD
PD
∴在Rt△ABP中,![]() ,
,
∴GH=![]() .
.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在反比例函数
在反比例函数![]() 的图象上,过点
的图象上,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.

(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“a2≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式,例如:x2+4x+5=x2+4x+4+1=(x+2)2+1,∵(x+2)2≥0,∴(x+2)2+1≥1,∴x2+4x+5≥1.试利用“配方法”解决下列问题:
(1)填空:因为x2-4x+7=(x-_____)2+______,所以当x=_____时,代数式x2-4x+7有最_____(填“大”或“小”)值,这个最值为_______;
(2)比较代数式x2-2与6x-13的大小.
(3)试求2x2-3x+2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
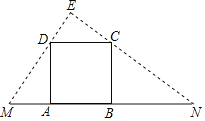
【题目】如图,在边长为6的正方形ABCD的一边AB在线段MN上移动,连接MD,NC并延长交于点E,MN=18.
(1)当AM=4时,求CN长;
(2)若∠E=90°,求证AM=BN;
(3)△MNE能否为等腰三角形?若能,求出AM的长,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:点B1的坐标为______;线段A1A2的长为______;△An-1BnAn的面积为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
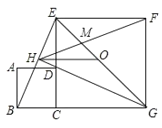
【题目】如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB=1+![]() :1,其中正确结论的序号为_________.
:1,其中正确结论的序号为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数![]() 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.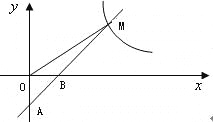
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上,修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的甬道,设甬道的宽为a米.
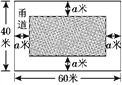 ①
①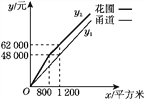 ②
②
(1)用含a的式子表示花圃的面积;
(2)如果甬道所占面积是整个长方形空地面积的![]() ,求此时甬道的宽;
,求此时甬道的宽;
(3)已知某园林公司修建甬道、花圃的造价y1(元)、y2(元)与修建面积x(平方米)之间的函数关系如图②所示.如果学校决定由该公司承建此项目,并要求修建的甬道宽不少于2米且不超过10米,那么甬道的宽为多少米时,修建的甬道和花圃的总造价最低?最低总造价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com