练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．计算或化简：
    （1）（-1）2015-2-1+（π-3.14）0
    （2）a3﹒a3+（-2a3）2-a8÷a2
    （3）-5x（-x2+2x+1）-（2x-3）（5+x2）
    （4）（x+3y-4z）（x-3y+4z）

    分析 （1）根据零指数幂和负整数指数幂计算即可；
    （2）根据整式的混合计算解答即可；
    （3）根据整式的混合计算解答即可；
    （4）根据整式的混合计算解答即可．

    解答 解：（1）（-1）2015-2-1+（ π-3.14）0
    =-1-$\frac{1}{2}$+1
    =-$\frac{1}{2}$；
    （2）a3﹒a3+（-2 a3）2-a8÷a2
    =a6+4a6-a6
    =4a6
    （3）-5x（-x2+2x+1）-（2x-3）（5+x2）
    =5x3-10 x2-5x-（10 x+2x3-15-3 x2）
    =3 x3-7 x2-15x+15
    （4）（x+3y-4z）（x-3y+4z）
    =[x+（3y-4z）][x-（3y-4z）]
    =x2-（3y-4z）2
    =x2-9 y2+24 yz-16z2．

    点评 此题考查整式的混合计算，关键是根据整式的混合计算顺序解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．已知 （2x-4）2+|x+2y-8|=0，则（x-y）2016=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算：
    （1）（6$\sqrt{12}$-8$\sqrt{27}$）÷2$\sqrt{3}$；
    （2）4$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{2}}$+$\sqrt{8}$+$\sqrt{48}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

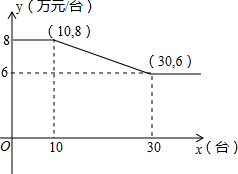    14．某公司销售智能机器人，售价每台为10万元，进价y与销售量x的函数关系式如图所示．
    （1）当x=10时，公司销售机器人的总利润为20万元；
    （2）当10≤x≤30时，求出y与x的函数关系式；
    （3）问：销售量为多少台时，公司销售机器人的总利润为37.5万元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

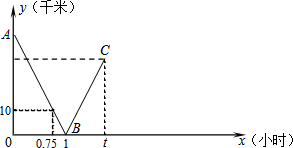    1．小明、小王二人骑车在平直的公路上分别从甲、乙两地相向而行，两人同时出发，匀速行驶．设行驶的时间为x（时），两人之间的距离为y（千米），小明到达乙地后立刻返回甲地，小王到达甲地后停止行驶，图中的折线表示从两人出发至小明到达乙地过程中y与x之间的函数关系．
    （1）根据图中信息，求甲乙两地之间的距离；
    （2）已知两人相遇时小明比小王多骑了4千米，若小明从甲地到达乙地所需时间为t时，求t的值；
    （3）请你在图中画出小明从乙地返回到甲地过程中y关于x的函数图象．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知A，B两地相距30km，甲骑自行车以15km/h的速度从A地到B地，同时，乙骑摩托车以30km/h的速度从B地到A地，到达A地后立即按原路原速返回，设甲、乙两人离B地的距离分别为y甲（km），y乙（km），行驶时间为t（h）．
    （1）分别写出y甲，y乙与t的函数关系式，并写出自变量的取值范围；
    （2）在同一坐标系中，（1）中的函数关系式对应的图象如图所示，请求出点C的坐标，并解释该点坐标所表示的实际意义；
    （3）若甲、乙两人的距离不超过3km时，能够用无线对讲机保持联系，直接写出两人能用无线对讲机保持联系时t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

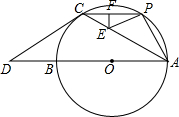    18．如图，AB是⊙O的直径，点C在⊙O上，过点C的切线交AB的延长线于点D，已知CD=CA．
    （1）求∠CAD的大小；
    （2）已知P是$\widehat{AC}$的中点，E是线段AC上一点（不含端点，且AE＞EC），作EF⊥PC，垂足为F，连接EP，当EF+EP的最小值为6时，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

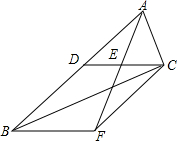    15．如图，四边形BFCD为平行四边形，点E是AF的中点．
    （1）求证：CF=AD；
    （2）若∠ACB=90°，试判断四边形BFCD的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

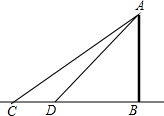    16．如图所示，对岸有一铁塔AB，在C处测得塔顶A的仰角为30°，向塔前进16米到达D，在D处测得A的仰角为40°，求铁塔AB的高．（结果保留整数）

    查看答案和解析>>

    同步练习册答案