练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

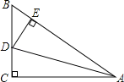
    【题目】如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，则下列结论.①AD平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④BE+AC=AB，其中正确的是____________

    【答案】①②④

    【解析】

    根据题中条件，结合图形及角平分线的性质得到结论，与各选项进行比对，排除错误答案，选出正确的结果．

    ∵AD平分∠BAC

    ∴∠DAC=∠DAE

    ∵∠C=90°，DE⊥AB

    ∴∠C=∠E=90°

    ∵AD=AD

    ∴△DAC≌△DAE

    ∴∠CDA=∠EDA

    ∴①AD平分∠CDE正确；

    根据已知条件无法证明∠BDE=∠ADE，

    ∴③DE平分∠ADB错误；

    ∵BE+AE=AB，AE=AC

    ∴BE+AC=AB

    ∴④BE+AC=AB正确；

    ∵∠BDE=90°∠B,∠BAC=90°∠B

    ∴∠BDE=∠BAC

    ∴②∠BAC=∠BDE正确.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】三角形内角和定理告诉我们：三角形三个内角的和等于180°．如何证明这个定理呢？

    我们知道，平角是180°，要证明这个定理就是把三角形的三个内角转移到一个平角中去，请根据如下条件，证明定理．

    （定理证明）

    已知：△ABC（如图①）．

    求证：∠A+∠B+∠C=180°．

    （定理推论）如图②，在△ABC中，有∠A+∠B+∠ACB=180°，点D是BC延长线上一点，由平角的定义可得∠ACD+∠ACB=180°，所以∠ACD= ．从而得到三角形内角和定理的推论：三角形的外角等于与它不相邻的两个内角的和．

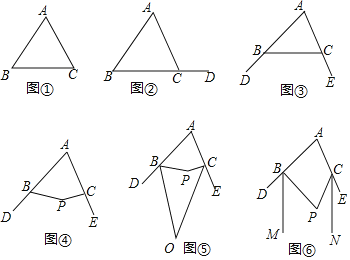
    （初步运用）如图③，点D、E分别是△ABC的边AB、AC延长线上一点．

    （1）若∠A=80°，∠DBC=150°，则∠ACB= ；

    （2）若∠A=80°，则∠DBC+∠ECB= ．

    （拓展延伸）如图④，点D、E分别是四边形ABPC的边AB、AC延长线上一点．

    （1）若∠A=80°，∠P=150°，则∠DBP+∠ECP= ；

    （2）分别作∠DBP和∠ECP的平分线，交于点O，如图⑤，若∠O=50°，则∠A和∠P的数量关系为 ；

    （3）分别作∠DBP和∠ECP的平分线BM、CN，如图⑥，若∠A=∠P，求证：BM∥CN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在中，平分交于点是上的一点(不与点重合)，于点．

    （1）若，如图1，当点与点重合时，求的度数；

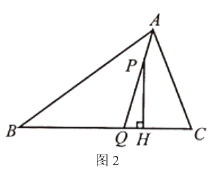
    （2）当是锐角三角形时，如图2，试探索之间的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校在“你最喜爱的课外活动项目”调查中，随机调查了若干名学生（每名学生分别选了一个活动项目），并根据调查结果绘制了如图所示的扇形统计图．已知“最喜爱机器人”的人数比“最喜爱3D打印”的人数少5人，则被调查的学生总人数为（ ）

    A.50人B.40人C.30人D.25人

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.

    (1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由；

    (2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何？请说明理由；

    (3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

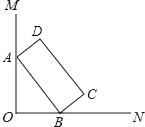
    【题目】如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，点不在同一条直线上，

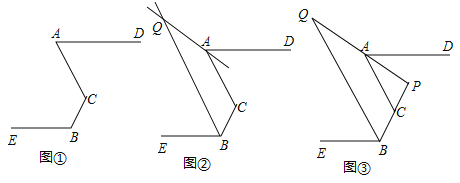
    （1）如图①，当时，求的度数；

    （2）如图②，分别为的平分线所在直线，试探究与的数量关系；

    （3）如图③，在（2）的前提下且，，直接写的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    （1）（﹣3y）（4x﹣3x2﹣1）；

    （2）（2x+3）（x﹣7）；

    （3）（-1）2019+（3-π）0 +2-2+ 4101×0.25100；

    （4）2019220182020．（运用乘法公式计算）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

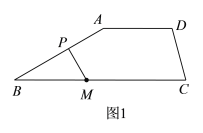
    【题目】已知：AD∥BC，点P为直线AB上一动点，点M在线段BC上，连接MP，，，．

    （1）如图1，当点P在线段AB上时，若，=150°，则=________°；

    （2）如图2，当点P在AB的延长线上时，写出，与之间的数量关系，并说明理由；

    （3）如图3，当点P在BA的延长线上时，请画出图形，直接写出，与之间的数量关系．

    查看答案和解析>>

    同步练习册答案