如图，是反比例函数
的图象的一支．根据给出的图象回答下列问题：
（1）该函数的图象位于哪几个象限？请确定m的取值范围；
（2）在这个函数图象的某一支上取点A（x1，y1）、B（x2，y2）．如果y1＜y2，那么x1与x2有怎样的大小关系？
（1）函数图象位于第二、四象限，m＜5。
（2）①当y1＜y2＜0时，x1＜x2；
②当0＜y1＜y2，x1＜x2。
解析试题分析：（1）根据反比例函数图象的对称性可知，该函数图象位于第二、四象限，则m﹣5＜0，据此可以求得m的取值范围；
（2）根据函数图象中“y值随x的增大而增大”进行判断。
解：（1）∵反比例函数图象关于原点对称，图中反比例函数图象位于第四象限，
∴函数图象位于第二、四象限，则m﹣5＜0，解得，m＜5。
∴m的取值范围是m＜5。
（2）由（1）知，函数图象位于第二、四象限，
∴在每一个象限内，函数值y随自变量x增大而增大。
①当y1＜y2＜0时，x1＜x2；
②当0＜y1＜y2，x1＜x2。
科目：初中数学 来源： 题型：填空题
如图，在平面直角坐标系
中，已知直线ｌ：
，双曲线
。在ｌ上取点A1，过点A1作
轴的垂线交双曲线于点B1，过点B1作
轴的垂线交于点A2，请继续操作并探究：过点A2作轴的垂线交双曲线于点B2，过点B2作轴的垂线交于点A3，…，这样依次得到上的点A1，A2，A3，…，An，…。记点An的横坐标为
，若
，则
= ，
= ；若要将上述操作无限次地进行下去，则
不能取的值是__________
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，矩形OABC的顶点B的坐标为(1，2)，反比例函数y＝
(0<m<2)的图象与AB交于点E，与BC交于点F，连接OE、OF、EF．
(1)若点E是AB的中点，则m＝ ，S△OEF＝ ；
(2)若S△OEF＝2S△BEF，求点E的坐标；
(3)是否存在点E及y轴上的点M，使得△MFE与△BFE全等?若存在，写出此时点E的坐标；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，点A，B分别在
轴，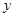
轴上，点D在第一象限内，DC⊥轴于点C，AO=CD=2，AB=DA=
，反比例函数
的图象过CD的中点E。
（1）求证：△AOB≌△DCA；
（2）求
的值；
（3）△BFG和△DCA关于某点成中心对称，其中点F在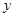轴上，试判断点G是否在反比例函数的图象上，并说明理由。（
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，在平面直角坐标系中，反比例函数
的图象和矩形ABCD在第二象限，AD平行于x轴，且AB=2，AD=4，点C的坐标为（-2，4）．
（1）直接写出A、B、D三点的坐标；
（2）若将矩形只向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，求反比例函数的解析式和此时直线AC的解析式y=mx+n．并直接写出满足
的x取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，反比例函数
的图象与一次函数y=kx+b的图象相交于两点A（m，3）和B（﹣3，n）．
（1）求一次函数的表达式；
（2）观察图象，直接写出使反比例函数值大于一次函数值的自变量x的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
(x＞0)的图象经过等腰梯形OABC的点A与BC的中点D．若等腰梯形OABC的面积为6，则k的值为 
经过点（2，﹣3），则k= ．
（k＞0）上，则a、b、c的大小关系为 （用“＜”将a、b、c连接起来）．