
【题目】已知:如图,抛物线y=ax2+bx+c与x轴相交于点B(1,0)和点C(9,0)两点,与y轴的负半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴正半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.
(1)求点A坐标和⊙P的半径;
(2)求抛物线的解析式;
(3)当△MOB与以点B、C、D为顶点的三角形相似时,求△CDN的面积.
【答案】
(1)
解:如图1所示:过点P作PE⊥BC,垂足为E.

∵PE⊥BC,
∴BE=EC=4.
∴OE=5.
∵⊙P与y轴相切,
∴PA⊥y轴.
∵∠PAO=∠AOE=∠OEP=90°,
∴四边形AOEP为矩形.
∴AP=OE=5,AO=EP.
∴⊙P的半径为5.
在Rt△BEP中,PE= ![]() =
= ![]() =3.
=3.
∴OA=3.
∴点A的坐标为(0,﹣3)
(2)
解:设抛物线的解析式为y=a(x﹣1)(x﹣9),将点A的坐标代入得:9a=﹣3,解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x2
x2 ![]() x﹣3
x﹣3
(3)
解:如图2所示:当直线MB经过点P时.

∵BD为⊙P的直径,
∴∠BCD=90°.
∴∠BCD=∠MOB=90°.
又∵∠MBO=∠CBD,
∴△MOB∽△DCB.
设MB的解析式为y=kx+b,将点B和点D的坐标代入得 ![]() ,解得:k=﹣
,解得:k=﹣ ![]() ,b=
,b= ![]() .
.
∴直线MB的解析式为y=﹣ ![]() x+
x+ ![]() .
.
将x=9代入得y=﹣6.
∴CD=6.
将y=﹣ ![]() x+
x+ ![]() 与y=﹣
与y=﹣ ![]() x2
x2 ![]() x﹣3联立解得:x=1或x=
x﹣3联立解得:x=1或x= ![]() .
.
△CDN的面积= ![]() DC(xN﹣xD)=
DC(xN﹣xD)= ![]() ×6×
×6× ![]() =
= ![]()
【解析】(1)过点P作PE⊥BC,垂足为E,连结AP.依据垂径定理可知BE=EC=4则OE=5,然后再证明四边形AOEP为矩形可求得到AP=OE=5,在Rt△BEP中,依据勾股定理可求得PE的长;(2)设抛物线的解析式为y=a(x﹣1)(x﹣9),将点A的坐标代入求解即可;(3)△MOB为直角三角形,则△BDC为直角三角形,故此只存在∠BCD为直角的情况,则MB经过点P,然后求得MB的解析式,将直线BM的解析式与抛物线的解析式组成方程组可求得点N的坐标,然后依据CD∥y轴可求得点CD的长,最后依据△CDN的面积= ![]() DC(xN﹣xD)求解即可.
DC(xN﹣xD)求解即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】下列判断正确的是( )
A.“打开电视机,正在播NBA篮球赛”是必然条件
B.“掷一枚硬币正面朝上的概率是 ![]() ”表示每掷硬币2次就必有1次反面朝上.
”表示每掷硬币2次就必有1次反面朝上.
C.一组数据2,3,4,5,5,6的众数和中位数都是5
D.若甲组数据的方差S甲2=0.24,乙组数据的方差S乙2=0.03,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
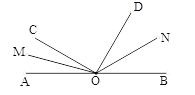
【题目】如图所示,∠AOB是平角,OM、ON分别是∠AOC、∠BOD 的平分线.
(1)知∠AOC=40°,∠BOD=60°,求∠MON的度数;
(2)知∠COD=90°,求出∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P为线段AB上的动点(与A、B两点不重合),在同一平面内,把线段AP、BP分别折成等边△CDP和△EFP,且D、P、F三点共线,如图所示. 
(1)若DF=2,求AB的长;
(2)若AB=18时,等边△CDP和△EFP的面积之和是否有最大值,如果有最大值,求最大值及此时P点位置,若没有最大值,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于灯塔P的北偏东30°方向,距离灯塔18海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东55°方向上的B处,此时渔船与灯塔P的距离约为海里(结果取整数)(参考数据:sin55°≈0.8,cos55°≈0.6,tan55°≈1.4).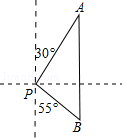
查看答案和解析>>
科目:初中数学 来源: 题型:
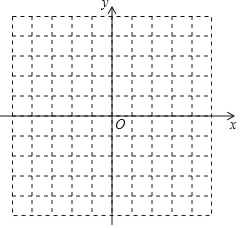
【题目】在平面直角坐标系中,点A(1,1),B(4,3),将点A向左平移2个单位长度,再向上平移3个单位长度得到点C.
(1)写出点C的坐标;
(2)画出△ABC并判断△ABC的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF. 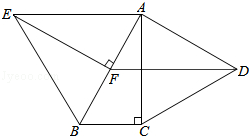
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com