
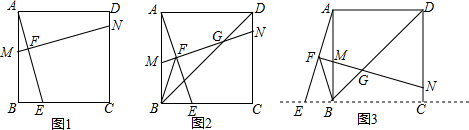
分析 (1)作辅助线,构建平行四边形PMND,再证明△ABE≌△DAP,即可得出结论;
(2)连接AG、EG、CG,构建全等三角形和直角三角形,证明AG=EG=CG,再根据四边形的内角和定理得∠AGE=90°,在Rt△ABE 和Rt△AGE中,利用直角三角形斜边上的中线等于斜边的一半得BF=$\frac{1}{2}$AE,FG=$\frac{1}{2}$AE,则BF=FG;
(3)①AE=MN,证明△AEB≌△NMQ;
②BF=FG,同理得出BF和FG分别是直角△AEB和直角△AGE斜边上的中线,则BF=$\frac{1}{2}$AE,FG=$\frac{1}{2}$AE,所以BF=FG.
解答 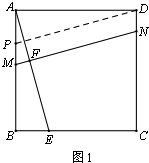 证明:(1)在图1中,过点D作PD∥MN交AB于P,则∠APD=∠AMN,
证明:(1)在图1中,过点D作PD∥MN交AB于P,则∠APD=∠AMN,
∵正方形ABCD,
∴AB=AD,AB∥DC,∠DAB=∠B=90°,
∴四边形PMND是平行四边形且PD=MN,
∵∠B=90°,
∴∠BAE+∠BEA=90°,
∵MN⊥AE于F,
∴∠BAE+∠AMN=90°,
∴∠BEA=∠AMN=∠APD,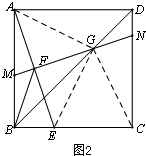
又∵AB=AD,∠B=∠DAP=90°,
∴△ABE≌△DAP,
∴AE=PD=MN;
(2)在图2中,连接AG、EG、CG,
由正方形的轴对称性△ABG≌△CBG,
∴AG=CG,∠GAB=∠GCB,
∵MN⊥AE于F,F为AE中点,
∴AG=EG,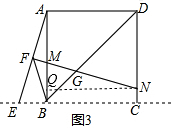
∴EG=CG,∠GEC=∠GCE,
∴∠GAB=∠GEC,
由图可知∠GEB+∠GEC=180°,
∴∠GEB+∠GAB=180°,
又∵四边形ABEG的内角和为360°,∠ABE=90°,
∴∠AGE=90°,
在Rt△ABE 和Rt△AGE中,AE为斜边,F为AE的中点,
∴BF=$\frac{1}{2}$AE,FG=$\frac{1}{2}$AE,
∴BF=FG;
(3)①AE与 MN的数量关系是:AE=MN,理由是:
如图3,过N作NQ⊥AB于Q,
∵∠NMQ=∠AMF,∠AMF=∠AEB,
∴∠AEB=∠NMQ,
∵AB=BC=QN,∠ABE=∠NQM=90°,
∴△AEB≌△NMQ,
∴AE=MN;
②BF与FG的数量关系是:BF=FG,
理由是:如图4,连接AG、EG、CG,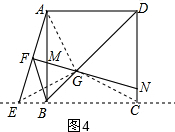
同理得:∠GAD=∠GCD,∠GEC=∠GCE,
∵∠GCE+∠GCD=90°,
∴∠GAD+∠GEC=90°,
∵AD∥EC,
∴∠DAE+∠AEC=180°,
∴∠AEG+∠EAG=90°,
∴∠AGE=90°,
在Rt△ABE 和Rt△AGE中,AE为斜边,F为AE的中点,
∴BF=$\frac{1}{2}$AE,FG=$\frac{1}{2}$AE,
∴BF=FG.
点评 本题是四边形的综合题,考查了正方形、全等三角形、平行四边形的性质和判定,在有中点和直角三角形的前提条件下,可以利用直角三角形斜边上的中线等于斜边的一半来证明两条线段相等.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
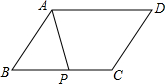 如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,
如图,在平行四边形ABCD中,点P是BC边的中点,设$\overrightarrow{CD}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b$,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com