
分析 先求出三项所占的百分比,再求出它们分别对的圆心角,然后作出扇形统计图即可.
解答 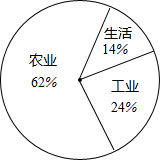 解:农业用水:$\frac{3.66×1{0}^{12}}{5.91×1{0}^{12}}$×100%≈62%,
解:农业用水:$\frac{3.66×1{0}^{12}}{5.91×1{0}^{12}}$×100%≈62%,
62%×360°≈223°,
工业用水:$\frac{1.40×1{0}^{12}}{5.91×1{0}^{12}}$×100%≈24%,
24%×360°≈86°,
生活用水:$\frac{8.27×1{0}^{11}}{5.91×1{0}^{12}}$×100%≈14%,
14%×360°≈51°.
点评 本题考查扇形统计图及相关计算.在扇形统计图中,每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
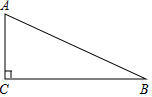 已知△ABC中,∠C=90°,AC=8cm,AB=17cm.
已知△ABC中,∠C=90°,AC=8cm,AB=17cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
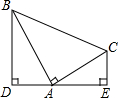 如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足为D,E,
如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,垂足为D,E,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
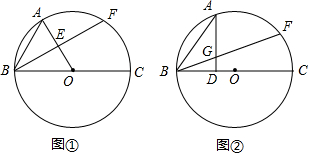
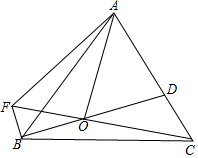 如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.
如图,点O为等边△ABC内一点,OA=2$\sqrt{5}$,OC=$\sqrt{15}$,连接BO并延长交AC于点D.若∠DOC=30°,过点B作BF⊥BD交CO延长线于点F,连接AF,则AF=$\frac{4\sqrt{15}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com