
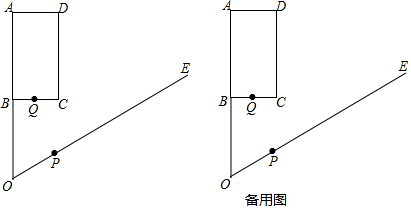
分析 (1)在直角△OBC中,先根据锐角的正切求∠BOC的度数;根据垂线段最短可知:当AP⊥OP时,PA的值最小,根据三角函数求AP的最小值;
(2)如图2,作辅助线,构建矩形PCBN,确定⊙P与线段OA围成的封闭图形是大弓形OM和小严凯弓形OM,根据扇形面积减去三角形面积可得结论;
(3)分三种情况:
①当⊙P与矩形ABCD的边BC相切时,是(2)问中的情况,此时t=$\frac{2\sqrt{3}}{3}$;
②当⊙P与矩形ABCD的边AD相切时,如图3,根据AN+NO=AO列式可得t的值;
③当⊙P与矩形ABCD的边CD相切时,如图4,根据PM+PH=BC列式可得t的值.
解答  解:(1)如图1,∵四边形ABCD是矩形,
解:(1)如图1,∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠OBC=90°,
tan∠BOC=$\frac{BC}{OB}$=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠BOC=30°,
当AP⊥OP时,PA的值最小,
∵OA=AB+OB=4+2$\sqrt{3}$,
在Rt△AOP中,∵∠AOE=60°,
∴sin60=$\frac{AP}{OA}$,
∴AP=$\frac{\sqrt{3}}{2}$×$(4+2\sqrt{3})$=2$\sqrt{3}$+3;
则PA的最小值是2$\sqrt{3}$+3;
故答案为:30°,2$\sqrt{3}$+3;
(2)如图2,由题意得:OP=半径r=2t,
连接PC、PM,则PC=PM=PO=r=2t,
∴∠POC=∠PCO=∠BOP-∠BOC=60°-30°=30°,
∵∠BCO=90°-∠BOC=90°-30°=60°,
∴∠PCB=∠BCO+∠PCO=60°+30°=90°,
即半径PC⊥BC(此时直线BC与⊙P相切),
作PN⊥OM于M,
∴∠PNB=∠NBC=∠BCP=90°,
∴四边形PCBN是矩形,
∴BN=PC=2t,
∵∠NOP=60°,
∴在Rt△PNO中,∠OPN=30°,
∴ON=$\frac{1}{2}$OP=t,
∵BN+ON=BO,
∴2t+t=2$\sqrt{3}$,
∴t=$\frac{2\sqrt{3}}{3}$,r=$\frac{4\sqrt{3}}{3}$,
∴当t=$\frac{2\sqrt{3}}{3}$时,⊙P经过点C,
S小弓形OM=S扇形POM-S△POM,
∵∠POM=60°且PO=PM,
∴△POM是等边三角形,
∴OM=2ON=2t=$\frac{4\sqrt{3}}{3}$,PN=$\sqrt{3}$t=2,
∴S小弓形OM=$\frac{60π•(\frac{4\sqrt{3}}{3})^{2}}{360}$-$\frac{1}{2}$×$\frac{4\sqrt{3}}{3}$×2=$\frac{8}{9}$π-$\frac{4}{3}\sqrt{3}$,
S大弓形OM=S圆P-S小弓形OM=π×$(\frac{4\sqrt{3}}{3})^{2}$-($\frac{8}{9}$π-$\frac{4}{3}\sqrt{3}$)═$\frac{8}{9}$π+$\frac{4}{3}\sqrt{3}$,
答:⊙P与线段OA围成的封闭图形的面积为$\frac{8}{9}$π-$\frac{4}{3}\sqrt{3}$或$\frac{8}{9}$π+$\frac{4}{3}\sqrt{3}$;
(3)①当⊙P与矩形ABCD的边BC相切时,是(2)问中⊙P过点C,此时t=$\frac{2\sqrt{3}}{3}$;
②当⊙P与矩形ABCD的边AD相切时,如图3,
过P作PF⊥AD于F,过P作PN⊥AO于N,
AN=FP=r=2t,
ON=$\frac{1}{2}$OP=t,
∵AN+NO=AO,
∴2t+t=2$\sqrt{3}$+4,
t=$\frac{4+2\sqrt{3}}{3}$,
③当⊙P与矩形ABCD的边CD相切时,如图4,
过PM⊥DC于M,交OA于H,
则PM=OP=2t,
PH=$\sqrt{3}$t,
∵PM+PH=BC,
∴2t+$\sqrt{3}$t=2,
t=4-2$\sqrt{3}$,
综上所述,当⊙P与矩形ABCD的边所在直线相切时t的值是$\frac{2\sqrt{3}}{3}$或$\frac{4+2\sqrt{3}}{3}$或4-2$\sqrt{3}$.
点评 本题是圆的综合题,考查了矩形的性质、垂线段的性质、直角三角形30°角的性质、弓形面积的计算、扇形面积公式、勾股定理、动点问题、直线与圆相切等知识,熟练掌握矩形的性质和直线与圆相切的性质是关键,第三问有难度,采用了分类讨论的思想解决问题,注意不要丢解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
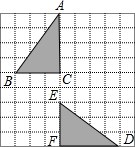 如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )
如图,在方格纸中,△ABC经过变换得到△DEF,正确的变换是( )| A. | 把△ABC向下平移4格,再绕点C逆时针方向旋转180° | |
| B. | 把△ABC向下平移5格,再绕点C顺时针方向旋转180° | |
| C. | 把△ABC绕点C逆时针方向旋转90°,再向下平移2格 | |
| D. | 把△ABC绕点C顺时针方向旋转90°,再向下平移5格 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
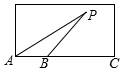 如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=$\frac{3}{5}$,求乙的游泳速度.
如图,甲乙两人在游泳池A处发现游泳池中的P处有人求救,甲立即跳入池中去救人,速度为1米/秒,乙以3.5米/秒的速度沿游泳池边跑到距A不远处的B处,捡起一个游泳圈再跳入池中去救人,甲游了20秒到达P处,两秒后乙到达P处.若∠PAB与∠PBC互余,且cos∠PBC=$\frac{3}{5}$,求乙的游泳速度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com