
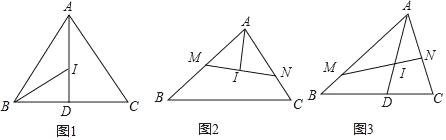
【题目】我们知道,三角形三个内角平分线的交点叫做三角形的内心,已知点I为△ABC的内心.
(1)如图1,连接AI并延长交BC于点D,若AB=AC=3,BC=2,求ID的长;
(2)如图2,过点I作直线交AB于点M,交AC于点N.
①若MN⊥AI,求证:MI2=BMCN;
②如图3,AI交BC于点D,若∠BAC=60°,AI=4,求![]() 的值.
的值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)如图1中,作IE⊥AB于E.设ID=x.由△BEI≌△BDI,可得ID=IE=x,BD=BE=1,AE=2,在Rt△AEI中,根据AE2+EI2=AI2,可得![]() 解方程即可;
解方程即可;
(2)如图2中,连接BI、CI.首先证明△AMI≌△ANI(ASA),再证明△BMI∽△INC,可得![]() ,推出NI2=BMCN,由此即可解决问题;
,推出NI2=BMCN,由此即可解决问题;
(3)过点N作NG∥AD交MA的延长线于G.由∠ANG=∠AGN=30°,推出AN=AG,![]() 由AI∥NG,推出
由AI∥NG,推出![]() ,可得
,可得![]() 即可推出
即可推出![]()
(1)如图1中,作IE⊥AB于E.设ID=x.
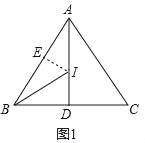
∵AB=AC=3,AI平分∠BAC,
∴AD⊥BC,BD=CD=1,
在Rt△ABD中,![]()
∵∠EBI=∠DBI,∠BEI=∠BDI=90°,BI=BI,
∴△BEI≌△BDI,
∴ID=IE=x,BD=BE=1,AE=2,
在Rt△AEI中,∵AE2+EI2=AI2,
∴![]()
∴![]()
∴![]()
(2)如图2中,连接BI、CI.
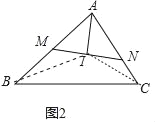
∵I是内心,
∴∠MAI=∠NAI,
∵AI⊥MN,
∴∠AIM=∠AIN=90°,
∵AI=AI,
∴△AMI≌△ANI(ASA),
∴∠AMN=∠ANM,
∴∠BMI=∠CNI,
设∠BAI=∠CAI=α,∠ACI=∠BCI=β,
∴∠NIC=90°﹣α﹣β,
∵∠ABC=180°﹣2α﹣2β,
∴∠MBI=90°﹣α﹣β,
∴∠MBI=∠NIC,
∴△BMI∽△INC,
∴![]()
∴NI2=BMCN,
∵NI=MI,
∴MI2=BMCN.
(3)过点N作NG∥AD交MA的延长线于G.

∴∠ANG=∠AGN=30°,
∴AN=AG,![]()
∵AI∥NG,
∴![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
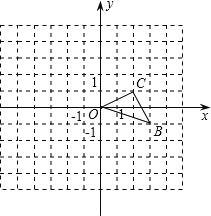
【题目】如图,已知O是坐标原点,B,C两点的坐标分别为(3,﹣1),(2,1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍,画出图形;
(2)分别写出B,C两点的对应点B′,C′的坐标;
(3)求△OB′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点
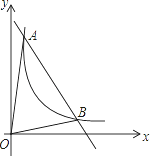
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<![]() 成立的x的取值范围;
成立的x的取值范围;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为12,E是边CD上一点,连接AE,折叠该纸片,使点A落在AE上的G点,并使折痕经过点B,得到折痕BF,点F在AD上,若DE=5,则GE的为_______________.
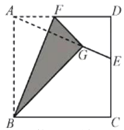
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com