
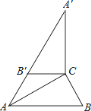
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C , 连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
A. 6 B. ![]() C.
C. ![]() D. 3
D. 3
【答案】A
【解析】
根据直角三角形的性质,可得AB的长,根据旋转的性质,可得A′B′的长,B′C的长,∠A′、∠A′B′C′,根据邻补角的定义,可得∠AB′C的度数,根据等腰三角形的判定,可得AB′,根据线段的和差,可得答案.
解:由在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,得
AB=4,∠BAC=30°.
由旋转的性质,得
A′B′=AB=4,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,AC=A′C.
由等腰三角形的性质,得
∠CAB′=∠A′=30°.
由邻补角的定义,得
∠AB′C=180°-∠A′B′C=120°.
由三角形的内角和定理,得
∠ACB′=180°-∠AB′C-∠B′AC=30°.
∴∠B′AC=∠B′CA=30°,
AB′=B′C=BC=2.
A′A=A′B′+AB′=4+2=6,
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
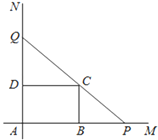
【题目】如图,互相垂直的两条公路AM、AN旁有一矩形花园ABCD,其中AB=30米,AD=20米.现欲将其扩建成一个三角形花园APQ,要求P在射线AM上,Q在射线AN上,且PQ经过点C.
(1)DQ=10米时,求△APQ的面积.
(2)当DQ的长为多少米时,△APQ的面积为1600平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
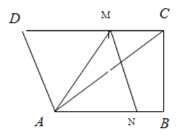
【题目】如图,在直角梯形ABCD中,AB∥DC,∠B=90°,AB=16,BC=12,CD=21.动点M从点C出发,沿射线CD方向以每秒2个单位长的速度运动;动点N从B出发,在线段BA上,以每秒1个单位长的速度向点A运动,点M、N分别从C、B同时出发,当点N运动到点A时,点M随之停止运动.设运动时间为t(秒).
(1)设△AMN的面积为S,求S与t之间的函数关系式,并确定t的取值范围;
(2)当t为何值时,以A、M、N三点为顶点的三角形是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 中,∠C=90°,将△ABC 绕点 C 顺时针旋转 90°,得到△DEC(其中点 D、E 分别是 A、B 两点旋转后的对应点).
(1)请画出旋转后的△DEC;
(2)试判断 DE 与 AB 的位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA 为⊙O 的切线,A 为切点,过 A 作弦 AB⊥OP,垂足为点 C,延长BO 与 PA 的延长线交于点 D
(1) 求证:PB 为⊙O 的切线
(2) 若 OB=3,OD=5,求 PB 的长
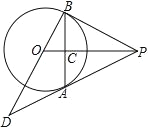
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至ED,连接AE、DE,△ADE的面积为3,求BC的长.
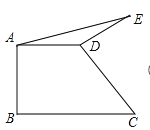
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按逆时针方向旋转n度后,得到△DEC,点D刚好落在AB边上,
(1)求n的值;
(2)若AC=4,求DF的长.
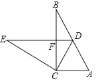
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过江汉平原的沪蓉(上海﹣成都)高速铁路即将动工.工程需要测量汉江某一段的宽度.如图①,一测量员在江岸边的A处测得对岸岸边的一根标杆B在它的正北方向,测量员从A点开始沿岸边向正东方向前进100米到达点C处,测得∠ACB=68°.
(1)求所测之处江的宽度(sin68°≈0.93,cos68°≈0.37,tan68°≈2.48.);
(2)除(1)的测量方案外,请你再设计一种测量江宽的方案,并在图②中画出图形.(不用考虑计算问题,叙述清楚即可)
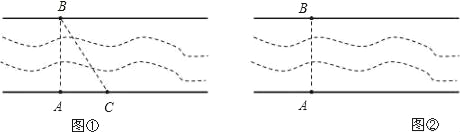
查看答案和解析>>
科目:初中数学 来源: 题型:
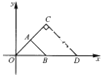
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com