
【题目】已知二次函数y=ax2+bx-3经过A(-1,0),B(3,0)两点,
(1)求二次函数解析式及对称轴方程;
(2)连接BC,交对称轴于点E,求E点坐标;
(3)在y轴上是否存在一点M,使ΔBCM为等腰三角形,若存在,直接写出点M的坐标,若不存在,请说明理由;
(4)在第四象限内抛物线上是否存一点H,使得四边形ACHB的面积最大,若存在,求出点H坐标,若不存在,说明理由.
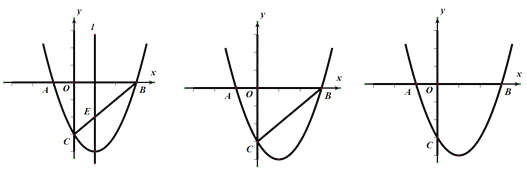
【答案】(1)二次函数解析式为y=x2-2x-3,对称轴方程为:直线x=1;
(2)E(1,-2);
(3)存在:M1(0,3),M2(0,0),M3(0,-3-![]() ),M4(0,-3+
),M4(0,-3+![]() )
)
(4)点H坐标为![]()
【解析】分析:(1)将A(-1,0)、B(3,0)代入二次函数y= ![]() ,求得a、b的值即可确定二次函数的解析式;(2)求出直线BC:y=x-3, 把对称轴方程直线x=1代入,即可求解;(3)在RT△BOC中,根据勾股定理求出BC,据等腰三角形的性质求出①当BC=BM时,M1(0,3);②当CM=BM时,点M与点O重合,M2(0,0);③当BC=CM时,M点有两个即M3(0,-3-
,求得a、b的值即可确定二次函数的解析式;(2)求出直线BC:y=x-3, 把对称轴方程直线x=1代入,即可求解;(3)在RT△BOC中,根据勾股定理求出BC,据等腰三角形的性质求出①当BC=BM时,M1(0,3);②当CM=BM时,点M与点O重合,M2(0,0);③当BC=CM时,M点有两个即M3(0,-3-![]() ),M4(0,-3+
),M4(0,-3+![]() );(4)设点H的坐标为
);(4)设点H的坐标为![]() ,连接OH,根据
,连接OH,根据![]() .
.
本题解析:(1)将A,B两点坐标代入y=ax2+bx-3得方程组,解得a=1,b=-2,所以二次函数解析式为y=x2-2x-3,对称轴方程为:直线x=1;
(2)设E点坐标为(1,a),把B(3,0),C(0,-3)代入直线BC:y=kx+b,求得解析式为:y=x-3, 把x=1,代入得:a=-2, ∴E(1,-2);
(3)存在:M1(0,3),M2(0,0),M3(0,-3-![]() ),M4(0,-3+
),M4(0,-3+![]() )
)
(4)连接OH,设H点坐标为(x0,x02-2x0-3)
S四边形ACHB=S△AOC+S△COH+S△BOH
=![]() +
+![]() x+
x+![]() |x02-2x0-3|
|x02-2x0-3|
=![]()
=![]()
当x0=![]() 时,x02-2x0-3=
时,x02-2x0-3=![]()
所以点H坐标为![]()



科目:初中数学 来源: 题型:
【题目】在 2008 年的一次抗震救灾大型募捐活动中,文艺工作者积极向灾区捐款.其中 10 人 的捐款分别是:5 万,8 万,10 万,10 万,10 万,20 万,20 万,30 万,50 万,100 万.这组数据的众数和中位数分别是( )
A. 10 万,15 万B. 10 万,20 万C. 20 万,15 万D. 20 万,10 万
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种细胞开始分裂时有两个,1小时后分裂成4个并死去一个,2小时后分裂成6个并死去一个,3小时后分裂成10个死去一个,按此规律,5小时后细胞存活的个数是( )
A. 31 B. 33 C. 35 D. 37
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮从A点出发前进8m,向右转45度,再前进8m,又向右转45度,…,这样一直走下去,他第一次回到出发点A时, 一共走了_____________ m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一人患了流感,经过两轮传染后共有64人患了流感.
(1)求每轮传染中平均一个人传染了几个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com