
【题目】如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于F,连接DE.

(1)求证:△ADE≌△CED
(2)若AD=4,AB=8,求△ACF的面积.
【答案】(1)见解析;(2)10.
【解析】
(1)根据矩形的性质可得出AD=BC、AB=CD,结合折叠的性质可得出AD=CE、AE=CD,进而即可证出△ADE≌△CED(SSS);
(2)由矩形的性质得出AB∥CD,CD=AB=8,∠ADC=90°,得出∠ACD=∠BAC,由折叠的性质得∠BAC=∠EAC,得出∠ACD=∠EAC,证出AF=CF,设AF=CF=x,则DF=CD-CF=8-x,在Rt△ADF中,由勾股定理得出方程,得出CF=5,由三角形面积公式即可得出答案.
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AB=CD.
由折叠的性质可得:BC=CE,AB=AE,
∴AD=CE,AE=CD.
在△ADE和△CED中,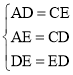 ,
,
∴△ADE≌△CED(SSS).
(2)解:∵四边形ABCD是矩形,
∴AB∥CD,CD=AB=8,∠ADC=90°,
∴∠ACD=∠BAC,
由折叠的性质得:∠BAC=∠EAC,
∴∠ACD=∠EAC,
∴AF=CF,
设AF=CF=x,则DF=CD﹣CF=8﹣x,
在Rt△ADF中,由勾股定理得:42+(8﹣x)2=x2,
解得:x=5,
∴CF=5,
∴△ACF的面积=![]() CF×AD=
CF×AD=![]() ×5×4=10.
×5×4=10.


科目:初中数学 来源: 题型:
【题目】某装备企业采用订单式生产销售某种产品,保证其销售量与产量相等,图中的线段![]() ,线段
,线段![]() 分别表示该产品每万台生产成本
分别表示该产品每万台生产成本![]() (单位:万元)、销售价
(单位:万元)、销售价![]() (单位:万元)与产量
(单位:万元)与产量![]() (单位:台)之间的函数关系,考虑企业的经济效益,当此种产品市场预定生产为
(单位:台)之间的函数关系,考虑企业的经济效益,当此种产品市场预定生产为![]() 万台时,将停止订单生产销售,求当该产品产量为多少万台时,可实现
万台时,将停止订单生产销售,求当该产品产量为多少万台时,可实现![]() 万元利润?
万元利润?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在完全重合放置的两张矩形纸片![]() 中,
中,![]() ,
,![]() ,将上面的矩形纸片折叠,使点
,将上面的矩形纸片折叠,使点![]() 与点
与点![]() 重合,折痕为
重合,折痕为![]() ,点
,点![]() 的对应点为
的对应点为![]() ,连接
,连接![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )

A. ![]() B. 6 C.
B. 6 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红与小刚姐弟俩做掷硬币游戏,他们两人同时各掷一枚壹元硬币.
![]() 若游戏规则为:当两枚硬币落地后正面朝上时,小红赢,否则小刚赢.请用画树状图或列表的方法,求小刚赢的概率;
若游戏规则为:当两枚硬币落地后正面朝上时,小红赢,否则小刚赢.请用画树状图或列表的方法,求小刚赢的概率;
![]() 小红认为上面的游戏规则不公平,于是把规则改为:当两枚硬币正面都朝上时,小红得
小红认为上面的游戏规则不公平,于是把规则改为:当两枚硬币正面都朝上时,小红得![]() 分,否则小刚得
分,否则小刚得![]() 分.那么,修改后的游戏规则公平吗?请说明理由;若不公平,请你帮他们再修改游戏规则,使游戏规则公平(不必说明理由).
分.那么,修改后的游戏规则公平吗?请说明理由;若不公平,请你帮他们再修改游戏规则,使游戏规则公平(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在一个长方形的草坪ABCD中,修了一条A-E-C的小路.AB=12米,BC=16米,AE=11米.极个别同学为了走“捷径”,沿着AC路线行走,破坏草坪.
(1)请求出小路EC段的长度;
(2)请求出实际上这些同学仅仅少走了多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com