
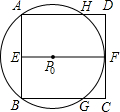
 装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点.
装置)P到达点P0处时,⊙P0与BC、EF、AD分别交于G、F、H点. -2)平方千米,当(探测装置)P从点P0出发继续前行多少千米到达点P1处时,A、B、C、D四点恰好在⊙P1上.
-2)平方千米,当(探测装置)P从点P0出发继续前行多少千米到达点P1处时,A、B、C、D四点恰好在⊙P1上.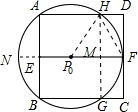
 HM=
HM= y,
y, y,
y, y.①
y.① HD•DF=
HD•DF= xy=2
xy=2 -2,②
-2,② -2,y=2.
-2,y=2. EF=y+x-
EF=y+x- (y+y+x)=
(y+y+x)= x,
x, -1(千米).
-1(千米). -1)千米到达P1时,A、B、C、D四点恰好在⊙P1上.
-1)千米到达P1时,A、B、C、D四点恰好在⊙P1上. HD•DF,就可以求出NE=MF的长.
HD•DF,就可以求出NE=MF的长.

科目:初中数学 来源: 题型:
 19、如图,矩形ABCD是供一辆机动车停放的车位示意图.请你参考图中数据(BC=2.2m,CD=5.4m,∠DCF=40°),计算车位所占街道的宽度EF.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1m.)
19、如图,矩形ABCD是供一辆机动车停放的车位示意图.请你参考图中数据(BC=2.2m,CD=5.4m,∠DCF=40°),计算车位所占街道的宽度EF.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1m.)查看答案和解析>>
科目:初中数学 来源: 题型:
 19、某小区为解决小区居民停车难问题,在小区道路旁画停车位,按要求宽度不能超过3.5米,如图,矩形ABCD是供一辆机动车停放的车位设计示意图,请你参考图中数据,计算车位所占道路的宽度EF是否符合设计要求.
19、某小区为解决小区居民停车难问题,在小区道路旁画停车位,按要求宽度不能超过3.5米,如图,矩形ABCD是供一辆机动车停放的车位设计示意图,请你参考图中数据,计算车位所占道路的宽度EF是否符合设计要求.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com