
 如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,求平移后三个顶点的坐标.
如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,求平移后三个顶点的坐标.  名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 贵阳市某中学初一年级的学生参加军训,在一次野外生存训练中,教官将一包食品随意埋在如图所示的区域中(图中每个三角形的大小、形状完全相同).
贵阳市某中学初一年级的学生参加军训,在一次野外生存训练中,教官将一包食品随意埋在如图所示的区域中(图中每个三角形的大小、形状完全相同).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
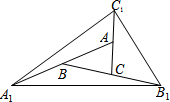 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,那么△A2B2C2的面积是( )
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,那么△A2B2C2的面积是( )| A. | 7 | B. | 14 | C. | 49 | D. | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将Rt△ABC沿BC方向平移得到△DEF,其中∠ABC=90°,AB=6,BC=8,S△MEC=$\frac{8}{3}$,则BE=$\frac{16}{3}$.
如图,将Rt△ABC沿BC方向平移得到△DEF,其中∠ABC=90°,AB=6,BC=8,S△MEC=$\frac{8}{3}$,则BE=$\frac{16}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2.即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A'B'C',并把它们拼成如图形状 (点C和A'重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.
在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2.即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A'B'C',并把它们拼成如图形状 (点C和A'重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等腰Rt△OAB中,∠OAB=90°,顶点A在y=-$\frac{12}{x}$(x<0)上,顶点B在y=$\frac{k}{x}$(x>0)上,若△OAB的面积是$\frac{25}{2}$,则k的值是7.
如图,等腰Rt△OAB中,∠OAB=90°,顶点A在y=-$\frac{12}{x}$(x<0)上,顶点B在y=$\frac{k}{x}$(x>0)上,若△OAB的面积是$\frac{25}{2}$,则k的值是7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com