
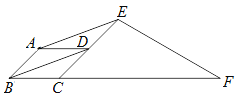
【题目】如图,在平行四边形ABCD中,∠ABC=45°,E、F分别在CD和BC的延长线上,AE∥BD,∠EFC=30°, AB=2.
求CF的长.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明进行了以下探索:设a+b
)2.善于思考的小明进行了以下探索:设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n均为整数),则有a+b
)2(其中a,b,m,n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.请你仿照小明的方法解决下列问题:
的式子化为平方式的方法.请你仿照小明的方法解决下列问题:
(1)当a,b,m,n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m,n的式子分别表示a,b,得a=______________,b=________;
)2,用含m,n的式子分别表示a,b,得a=______________,b=________;
(2)利用所探索的结论,找一组正整数a,b,m,n填空:
________+________![]() =(________+________
=(________+________![]() )2;
)2;
(3)若a+4![]() =(m+n
=(m+n![]() )2,且a,m,n均为正整数,求a的值.
)2,且a,m,n均为正整数,求a的值.
(4)试化简![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,四块阴影部分的面积分别为S1、S2、S3、S4.则S1+S2+S3+S4等于( )
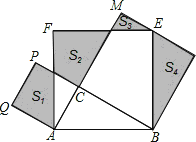
A.14 B.16 C.18 D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按照有关规定:距离铁轨道200米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.
如图是一个小区平面示意图,矩形ABEF为一新建小区,直线MN为高铁轨道,C、D是直线MN上的两点,点C、A、B在一直线上,且DA⊥CA,∠ACD=30°.小王看中了①号楼A单元的一套住宅,与售楼人员的对话如下:

(1)小王心中一算,发现售楼人员的话不可信,请你通过计算用所学的数学知识说明理由.
(2)若一列长度为228米的高铁以70米/秒的速度通过时,则A单元用户受到影响时间有多长?( 温馨提示:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈6.1)
≈6.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)3ab2(﹣![]() a2b)2abc;
a2b)2abc;
(2)(﹣![]() x2y)3(﹣3xy2);
x2y)3(﹣3xy2);
(3)(﹣3xy2)3(![]() x3y);
x3y);
(4)(x2+3x)﹣2(4x﹣x2).
查看答案和解析>>
科目:初中数学 来源: 题型:
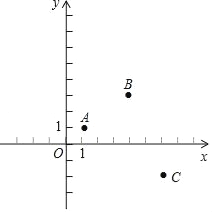
【题目】已知A(1,1),B(4,3),C(6,﹣2),在平面直角坐标找一点D,使以A、B、C、D四点的四边形为平行四边形,则D点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com