
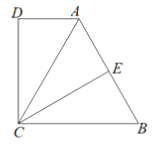
【题目】如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.
(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;
(2)当∠B=70°时,求∠AEC的度数;
(3)当△ACE为直角三角形时,求边BC的长.
【答案】(1)![]() ;(2)∠AEC=105°;(3)边BC的长为2或
;(2)∠AEC=105°;(3)边BC的长为2或![]() .
.
【解析】试题分析:(1)过A作AH⊥BC于H,得到四边形ADCH为矩形.在△BAH中,由勾股定理即可得出结论.
(2)取CD中点T,连接TE,则TE是梯形中位线,得ET∥AD,ET⊥CD,∠AET=∠B=70°.
又AD=AE=1,得到∠AED=∠ADE=∠DET=35°.由ET垂直平分CD,得∠CET=∠DET=35°,即可得到结论.
(3)分两种情况讨论:①当∠AEC=90°时,易知△CBE≌△CAE≌△CAD,得∠BCE=30°,
解△ABH即可得到结论.
②当∠CAE=90°时,易知△CDA∽△BCA,由相似三角形对应边成比例即可得到结论.
试题解析:解:(1)过A作AH⊥BC于H.由∠D=∠BCD=90°,得四边形ADCH为矩形.
在△BAH中,AB=2,∠BHA=90°,AH=y,HB=![]() ,∴
,∴![]() ,
,
则![]()
(2)取CD中点T,联结TE,则TE是梯形中位线,得ET∥AD,ET⊥CD,∴∠AET=∠B=70°.
又AD=AE=1,∴∠AED=∠ADE=∠DET=35°.由ET垂直平分CD,得∠CET=∠DET=35°,∴∠AEC=70°+35°=105°.
(3)分两种情况讨论:①当∠AEC=90°时,易知△CBE≌△CAE≌△CAD,得∠BCE=30°,
则在△ABH中,∠B=60°,∠AHB=90°,AB=2,得BH=1,于是BC=2.
②当∠CAE=90°时,易知△CDA∽△BCA,又![]() ,
,
则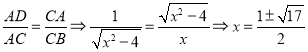 (舍负)
(舍负)
易知∠ACE<90°,所以边BC的长为![]() .
.
综上所述:边BC的长为2或![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本,小亮用31元买了同样的钢笔2支和笔记本5本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔和笔记本共48件作为奖品,奖给校运会表现突出的同学,要求笔记本数不少于钢笔数.请问:有多少购买方案?请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
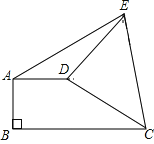
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC, AD=3,将腰CD以D为中心逆时针旋转90°至DE,连接AE、CE,![]() AED的面积为6,则BC的长为_____.
AED的面积为6,则BC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 、
、![]() ,且
,且![]() ,与
,与![]() 轴的正半轴的交点在
轴的正半轴的交点在![]() 的下方.下列结论:①
的下方.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数是( )个.
.其中正确结论的个数是( )个.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图1,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.
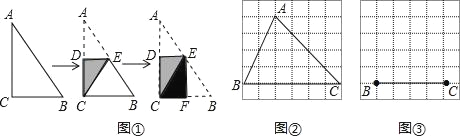
(1)如图2,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕;
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是 ;
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣5,﹣2,1,9,且任意相邻四个台阶上数的和都相等.
尝试 (1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用 求从下到上前31个台阶上数的和.
发现 试用含k(k为正整数)的式子表示出数“1”所在的台阶数.

查看答案和解析>>
科目:初中数学 来源: 题型:
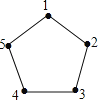
【题目】如图,一个正五边形的五个顶点依次编号为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从某个顶点开始,若顶点编号是奇数,则一次逆时针走
,从某个顶点开始,若顶点编号是奇数,则一次逆时针走![]() 个边长;若顶点编号是偶数,则一次顺时针走
个边长;若顶点编号是偶数,则一次顺时针走![]() 个边长.若从编号
个边长.若从编号![]() 开始走,则第
开始走,则第![]() 次后,所处顶点编号是_____________.
次后,所处顶点编号是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六个数:0.123,![]() ,3.1416,﹣2π,(﹣1.5)3,0.1020020002(相邻两个2之间0的个数逐次加1),若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=_____
,3.1416,﹣2π,(﹣1.5)3,0.1020020002(相邻两个2之间0的个数逐次加1),若其中无理数的个数为x,整数的个数为y,非负数的个数为z,则x+y+z=_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com