
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE
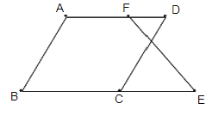
证明:∵∠B+∠BCD=180°(已知)
∴AB∥CD( )
∴∠B=∠DCE( )
又∵∠B=∠D(已知 ),
∴___________ (等量代换)
∴ ∥
∴∠E=∠DFE( )
【答案】同旁内角互补,两直线平行;两直线平行,同位角相等;∠DCE=∠D;AD;BE;两直线平行,内错角相等
【解析】
根据平行线的判定得出AB∥CD,根据平行线的性质得出∠B=∠DCE,求出∠DCE=∠D,根据平行线的判定得出AD∥BE,根据平行线的性质得出即可.
证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行),
∴∠B=∠DCE(两直线平行,同位角相等),
∵∠B=∠D(已知),
∴∠DCE=∠D(等量代换),
∴AD∥BE( 内错角相等,两直线平行),
∴∠E=∠DFE(两直线平行,内错角相等),
故答案为:同旁内角互补,两直线平行;两直线平行,同位角相等;∠DCE=∠D;AD;BE;两直线平行,内错角相等.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线y= ![]() x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
x2﹣3x+m与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为(、),BK的长是 , CK的长是;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2 , 在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。

(1)求证:四边形CMAN是平行四边形。
(2)已知DE=4,FN=3,求BN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为 ( )
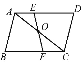
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
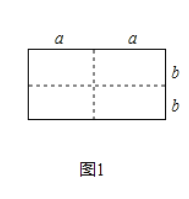
![]() 图2中的阴影部分的正方形的边长是 .
图2中的阴影部分的正方形的边长是 .
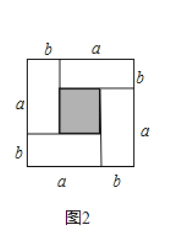
![]() 请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:
请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:![]() 之间的等量关系;
之间的等量关系;
![]() 利用
利用![]() 中的结论计算:
中的结论计算:![]() ,求
,求![]() 的值;
的值;
![]() 根据
根据![]() 中的结论,直接写出
中的结论,直接写出![]() 和
和![]() 之间的关系;若
之间的关系;若![]() ,分别求出
,分别求出![]() 和
和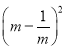 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,以下四个结论:①a>0;②c>0;③b2﹣4ac>0;④﹣ ![]() <0,正确的是( )
<0,正确的是( )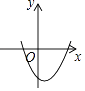
A.①②
B.②④
C.①③
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2 , …,Bn , 以线段AnBn为边向左作正方形AnBnCnDn , 如果这组抛物线中的某一条经过点Dn , 求此时满足条件的正方形AnBnCnDn的边长.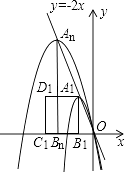
查看答案和解析>>
科目:初中数学 来源: 题型:
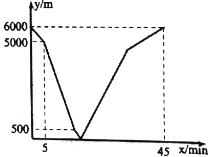
【题目】2019年3月31日,重庆举行了国际马拉松比赛,众多志愿者参与了服务工作,志愿者小茜和小悠分别从“南滨公园”和“朝天门桥”出发,沿同一条笔直的公路相向而行.小茜先出发5分钟后,小悠立刻骑自行车赶往“南滨公园”.小茜开始骑滑板车,中途改为跑步,且跑步的速度为滑板车速度的一半,到达“朝天门桥”时恰好用了45分钟.若两人之间的距离![]() 与小茜离开出发地的时间
与小茜离开出发地的时间![]() 之间的关系如图所示.则当小悠到达“南滨公园”时,小茜离“朝天门桥”的距离为__________米.
之间的关系如图所示.则当小悠到达“南滨公园”时,小茜离“朝天门桥”的距离为__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于6,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com