
分析 把x2+x-2进行因式分解,根据题意得到方程组,解方程组即可.
解答 解:∵x2+x-2=(x+2)(x-1),x2+x-2与2x-1分别是多项式ax3+bx2+cx-5,
∴x=-2或x=1时,ax3+bx2+cx-5=0,
即-8a+4b-2c-5=0,a+b+c-5=0,
∵2x-1是多项式ax3+bx2+cx-$\frac{25}{16}$的因式,
∴x=$\frac{1}{2}$时,ax3+bx2+cx-$\frac{25}{16}$=0,
即$\frac{1}{8}$a+$\frac{1}{4}$b+$\frac{1}{2}$c-$\frac{25}{16}$=0,
$\left\{\begin{array}{l}{-8a+4b-2c-5=0}\\{a+b+c-5=0}\\{\frac{1}{8}a+\frac{1}{4}b+\frac{1}{2}c-\frac{25}{16}=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=3}\\{c=\frac{3}{2}}\end{array}\right.$.
所以a=$\frac{1}{2}$,b=3,c=$\frac{3}{2}$.
点评 本题考查的是因式分解的意义,根据题意列出关于a、b、c的三元一次方程组是解题的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
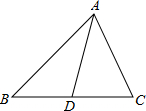 如图,在△ABC中,∠B=45°,∠C=75°,AD是△ABC的角平分线,则∠ADC的度数是( )
如图,在△ABC中,∠B=45°,∠C=75°,AD是△ABC的角平分线,则∠ADC的度数是( )| A. | 75° | B. | 95° | C. | 105° | D. | 115° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知BC∥DE,则下列说法不正确的是( )
如图,已知BC∥DE,则下列说法不正确的是( )| A. | 两个三角形是位似图形 | B. | 点A是两个三角形的位似中心 | ||
| C. | AE:AD是相似比 | D. | 点B与点E,点C与点D是对应位似点 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
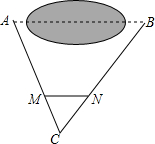 如图,A、B两点分别位于一个池塘的两端,为了测量A、B之间的距离,小天想了一个办法:在地上取一点C,使它可以直接到达A﹑B两点,连接AC、BC,在AC上取一点M,使AM=3MC,作MN∥AB交BC于点N,测得MN=38m,则A、B两点间的距离为( )
如图,A、B两点分别位于一个池塘的两端,为了测量A、B之间的距离,小天想了一个办法:在地上取一点C,使它可以直接到达A﹑B两点,连接AC、BC,在AC上取一点M,使AM=3MC,作MN∥AB交BC于点N,测得MN=38m,则A、B两点间的距离为( )| A. | 76m | B. | 95m | C. | 114m | D. | 152m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com