
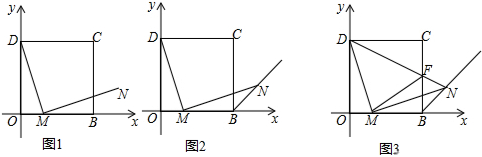
分析 (1)如图1中,作NE⊥OB于E,只要证明△DMO△MNE即可解决问题.
(2)如图2中,在OD上取OH=OM,连接HM,只要证明△DHM≌△MBN即可.
(3)结论:MN平分∠FMB成立.如图3中,在BO延长线上取OA=CF,过M作MP⊥DN于P,因为∠NMB+∠CDF=45°,所以只要证明∠FMN+∠CDF=45°即可解决问题.
解答 (1)解:如图1中,作NE⊥OB于E,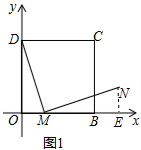
∵∠DMN=90°,
∴∠DMO+∠NME=90°,∠NME+∠MNE=90°,
∴∠DMO=∠MNE,
在△DMO和△MNE中,
$\left\{\begin{array}{l}{∠DOM=∠NEM=90°}\\{∠DMO=∠MNE}\\{DM=MN}\end{array}\right.$,
∴△DMO△MNE,
∴ME=DO=2,NE=OM=a,
∴OE=OM+ME=2+a,
∴点N坐标(2+a,a),
故答案为N(2+a,a).
(2)证明:如图2中,在OD上取OH=OM,连接HM,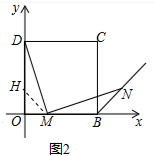
∵OD=OB,OH=OM,∴HD=MB,∠OHM=∠OMH,
∴∠DHM=180°-45°=135°,
∵NB平分∠CBE,∴∠NBE=45°,
∴∠NBM=180°-45°=135°,∴∠DHM=∠NBM,
∵∠DMN=90°,∴∠DMO+∠NMB=90°,
∵∠HDM+∠DMO=90°,
∴∠HDM=∠NMB,
在△DHM和△MBN中,
$\left\{\begin{array}{l}{∠HDM=∠NMB}\\{DH=MB}\\{∠DHM=∠NBM}\end{array}\right.$,
∴△DHM≌△MBN(ASA),
∴DM=MN.
(3)结论:MN平分∠FMB成立.
证明:如图3中,在BO延长线上取OA=CF,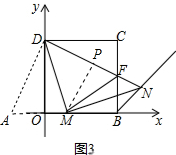
在△AOD和△FCD中,
$\left\{\begin{array}{l}{DO=DC}\\{∠DOA=∠C=90°}\\{OA=CF}\end{array}\right.$
∴△DOA≌△DCF,
∴AD=DF,∠ADO=∠CDF,
∵∠MDN=45°,
∴∠CDF+∠ODM=45°,
∴∠ADO+∠ODM=45°,
∴∠ADM=∠FDM,
在△DMA和△DMF中,
$\left\{\begin{array}{l}{DM=DM}\\{∠MDA=∠MDF}\\{DA=DF}\end{array}\right.$,
∴△DMA≌△DMF,
∴∠DFM=∠DAM=∠DFC,
过M作MP⊥DN于P,则∠FMP=∠CDF,
由(2)可知∠NMF+∠FMP=∠PMN=45°,
∵∠NMB=∠MDO,∠MDO+∠CDF=45°,
∴∠NMB=∠NMF,即MN平分∠FMB.
(在旋转过程中,FM=AM,显然AM的长度是变化的,故FM的长度是变化的或取两个特殊位置,比较AM的值即可发现结论).
点评 本题考查四边形综合题、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是学会添加辅助线,构造全等三角形,记住一些基本图形,可以使得我们在观察新问题的时候很迅速地联想,属于中考压轴题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
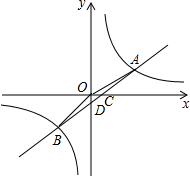 已知:如图所示,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数$y=\frac{k}{x}(k≠0)$的图象交于一、三象限内的A、B两点,与x交于点C,与y轴交于点D,OC=1,BC=5,$sin∠BCO=\frac{3}{5}$.
已知:如图所示,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数$y=\frac{k}{x}(k≠0)$的图象交于一、三象限内的A、B两点,与x交于点C,与y轴交于点D,OC=1,BC=5,$sin∠BCO=\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=-$\frac{8}{x}$的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是-2.
如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数y2=-$\frac{8}{x}$的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
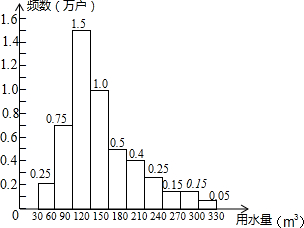 为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是( )
为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断合理的是( )| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2厘米 | B. | 3厘米 | C. | 4厘米 | D. | 5厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
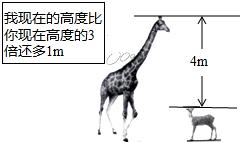 如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.
如图,根据图中的信息,若设长颈鹿的身高为xm,梅花鹿的身高为ym,则可列方程组$\left\{\begin{array}{l}{x-y=4}\\{x=3y+1}\end{array}\right.$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com