
 如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,
如图所示.有两个自由转动的均匀转盘A,B,都被分成了3等份,分析 (1)利用表格列举出所有的可能进而利用概率公式求出答案;
(2)游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
解答 解:(1)每次游戏可能出现的所有结果列表如下:
转盘B的数字 转盘A的数字 | 4 | 5 | 6 |
| 1 | (1,4) | (1,5) | (1,6) |
| 2 | (2,4) | (2,5) | (2,6) |
| 3 | (3,4) | (3,5) | (3,6) |
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:解答题
 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
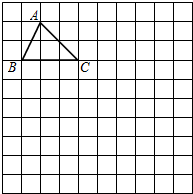 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{2}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在学校里随机调查 | B. | 在社会上随机调查 | ||
| C. | 普查 | D. | 抽样调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com