
【题目】平面直角坐标系中,对于点![]() 和点
和点![]() ,给出如下定义:
,给出如下定义:
若![]() 则称点
则称点![]() 为点
为点![]() 的可变点.例如:点
的可变点.例如:点![]() 的可变点的坐标是
的可变点的坐标是 ![]() ,点
,点![]() 的可变点的坐标是
的可变点的坐标是 ![]() .
.
(1)①点![]() 的可变点的坐标是 ;
的可变点的坐标是 ;
②在点![]() ,
,![]() 中有一个点是函数
中有一个点是函数![]() 图象上某一个点的可变点,这个点是 ;(填“A”或“B”)
图象上某一个点的可变点,这个点是 ;(填“A”或“B”)
(2)若点![]() 在函数
在函数 ![]() 的图象上,求其可变点
的图象上,求其可变点![]() 的纵坐标
的纵坐标![]() 的取值范围;
的取值范围;

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)连接BF,求证:CF=EF.
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其他条件不变,如图②,求证:AF+EF=DE.
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其他条件不变,如图③,你认为(2)中的结论还成立吗?若成立,写出证明过程;若不成立,请直接写出AF、EF与DE之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知![]() 是关于
是关于![]() 的方程
的方程![]() 的解,求
的解,求![]() 的值.
的值.
(2)已知关于x的方程![]() 的解与方程
的解与方程![]() 的解互为倒数,求
的解互为倒数,求![]() 的值.
的值.
(3)小丽在解关于![]() 的方程
的方程![]() 时,出现了一个失误:“在将
时,出现了一个失误:“在将![]() 移到方程的左边时,忘记了变号.”结果她得到方程的解为
移到方程的左边时,忘记了变号.”结果她得到方程的解为![]() ,求
,求![]() 的值和原方程的解.
的值和原方程的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。
(1)在图中画一个以AB为腰的等腰三角形△ABC,点C在小正方形的顶点上,且tan∠B=3;
(2)在图中画一个以AB为底的等腰三角形△ABD,点D在小正方形的项点上,且△ABD是锐角三角形.连接CD,请直接写出线段CD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见下表.若2015年5月份,该市居民甲用电100千瓦时,交电费60元.
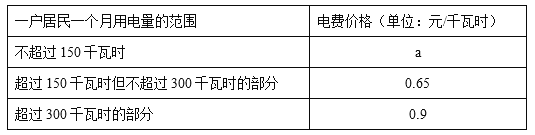
(1)上表中,a= ,若居民乙用电200千瓦时,交电费 元.
(2)若某用户某月用电量超过300千瓦时,设用电量为x千瓦时,请你用含x的代数式表示应交的电费.
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少千瓦时时,其当月的平均电价每千瓦时不超过0.62元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙0直径,C是⊙0外一点,连接BC交⊙0于点D,BD=CD,连接AD、AC.
(1)如图1,求证:∠BAD=∠CAD
(2)如图2,过点C作CF⊥AB于点F,交⊙0于点E,延长CF交⊙0于点G.过点作EH⊥AG于点H,交AB于点K,求证AK=2OF;
(3)如图3,在(2)的条件下,EH交AD于点L,若0K=1,AC=CG,求线段AL的长.

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)若![]() ,∠BCD=120°判断四边形
,∠BCD=120°判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们都知道任何一个非零数都有倒数,现定义:a是不为﹣1的有理数,我们把![]() 称为有理数a的和倒数.请根据上述定义,解决以下问题:
称为有理数a的和倒数.请根据上述定义,解决以下问题:
(1)求有理数2的和倒数;
(2)求有理数﹣5的和倒数;
(3)已知a1=1,a2是a1的和倒数,a3是a2的和倒数,a4是a3的和倒数,……,依此类推,求a10的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国高铁迅猛发展,给我们的出行带来极大的便捷,如图1,是某种新设计动车车头的纵截面一部分,曲线OBA是一开口向左,对称轴正好是水平线OC的抛物线的一部分,点A、B是车头玻璃罩的最高点和最低点,AC、BD是两点到车厢底部的距离,OD=1.5米,BD=1.5米,AC=3米,请你利用所学的函数知识解决以下问题.
(1)为了方便研究问题,需要把曲线OBA绕点O旋转转化为我们熟悉的函数,请你在所给的方框内,画出你旋转后函数图象的草图,在图中标出点O、A、B、C、D对应的位置,并求你所画的函数的解析式.
(2)如图2,驾驶员座椅安装在水平线OC上一点P处,实验表明:当PA+PB最小时,驾驶员驾驶时视野最佳,为了达到最佳视野,求OP的长.
(3)驾驶员头顶到玻璃罩的高度至少为0.3米才感到压抑,一个驾驶员坐下时头顶到椅面的距离为1米,在(2)的情况下,座椅最多条件到多少时他才感到舒适?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com