
【题目】如图,点![]() 在平行四边形
在平行四边形![]() 的对角线
的对角线![]() 上,过点
上,过点![]() 、
、![]() 分别作
分别作![]() 、
、![]() 的平行线相交于点
的平行线相交于点![]() ,连接
,连接![]() ,
,![]() .
.
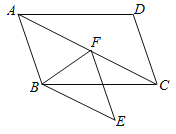
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析 (2)![]() +3
+3
【解析】
(1)由外角的性质可得∠AFB=∠FBC+∠FCB,又因为∠ABF=∠FBC+∠FCB,易得AB=AF,由菱形的判定定理可得结论;
(2)作DH⊥AC于点H,由特殊角的三角函数可得∠CBE=30°,由平行线的性质可得∠2=∠CBE=30°,利用锐角三角函数可得AH,DH,由菱形的性质和勾股定理得CH,得AC.
(1)证明:∵EF∥AB,BE∥AF,
∴四边形ABEF是平行四边形。
∵∠ABF=∠FBC+∠FCB,∠AFB=∠FBC+∠FCB,
∴∠ABF=∠AFB,
∴AB=AF,
∴ABEF是菱形;
(2)作DH⊥AC于点H,
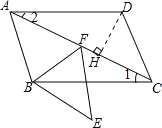
∵sin∠CBE=![]() ,
,
∴∠CBE=30,
∵BE∥AC,
∴∠1=∠CBE,
∵AD∥BC,
∴∠2=∠1,
∴∠2=∠CBE=30,
Rt△ADH中,AH=![]() =
=![]() ,
,
DH=![]() ∠2=4,
∠2=4,
∵四边形ABEF是菱形,
∴CD=AB=BE=5,
Rt△CDH中,CH=![]()
∴AC=AH+CH=![]() +3.
+3.
故答案为:![]() +3.
+3.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
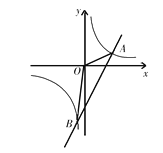
【题目】如图,直线y1=3x﹣5与反比例函数y2=![]() 的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
的图象相交A(2,m),B(n,﹣6)两点,连接OA,OB.
(1)求k和n的值;
(2)求△AOB的面积;
(3)直接写出y1> y2时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
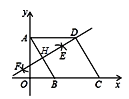
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0,![]() ),分别以A,B为圆心,大于
),分别以A,B为圆心,大于![]() AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
AB的长为半径作弧,两弧交于E,F两点,直线EF恰好经过点D,交AB于点H,则四边形HBCD的周长为( )
A.![]() B.6C.
B.6C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
①小亮测试成绩的平均数比小明的高;②小亮测试成绩比小明的稳定;③小亮测试成绩的中位数比小明的高;④小亮参加第一轮比赛,小明参加第二轮比赛,比较合理.
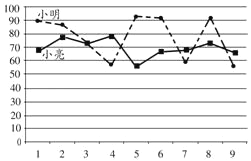
A. ①③B. ①④C. ②③D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点
,将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,求
,求![]() 的值;
的值;
(3)若抛物线![]() 与线段
与线段![]() 有且只有一个公共点时,求抛物线顶点横坐标
有且只有一个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,将点
,将点![]() 向右平移6个单位长度,得到点
向右平移6个单位长度,得到点![]() .
.
(1)直接写出点![]() 的坐标;
的坐标;
(2)若抛物线![]() 经过点
经过点![]() ,求
,求![]() 的值;
的值;
(3)若抛物线![]() 与线段
与线段![]() 有且只有一个公共点时,求抛物线顶点横坐标
有且只有一个公共点时,求抛物线顶点横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
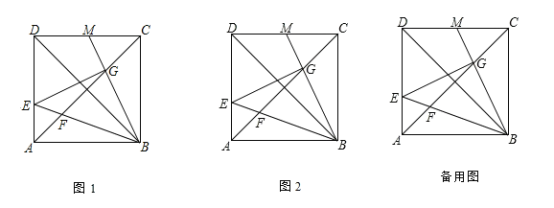
【题目】如图,在边长为6的正方形ABCD中,点E为AD边上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G、交CD于点M.
(1)如图1,联结BD,求证:![]() ,并写出
,并写出![]() 的值;
的值;
(2)联结EG,如图2,若设![]() ,求y关于
,求y关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当M为边DC的三等分点时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
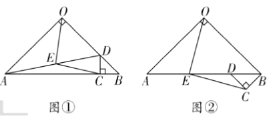
【题目】如图①,在![]() 中,
中,![]() 为
为![]() 边上一点,过
边上一点,过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(观察猜想)
(1)①![]() 的数量关系是___________
的数量关系是___________
②![]() 的数量关系是______________
的数量关系是______________
(类比探究)
(2)将图①中![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
,如图②所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(拓展迁移)
(3)将![]() 绕点
绕点![]() 旋转任意角度,若
旋转任意角度,若![]() ,请直接写出点
,请直接写出点![]() 在同一直线上时
在同一直线上时![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() 且经过点
且经过点![]() 动直线
动直线![]() 的解析式为
的解析式为![]()
![]() .
.
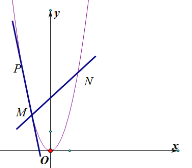
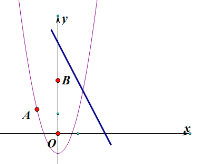
(1)求抛物线![]() 的解析式;
的解析式;
(2)将抛物线![]() 向上平移一个单位得到新的抛物线
向上平移一个单位得到新的抛物线![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点(
两点(![]() 点位于
点位于![]() 点的左边),动直线
点的左边),动直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 的另外一个交点为点
的另外一个交点为点![]() 求证:直线
求证:直线![]() 恒过一个定点;
恒过一个定点;
(3)已知点![]() ,且点
,且点![]() 在动直线
在动直线![]() 上,若
上,若![]() 是以
是以![]() 为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出
为顶角的等腰三角形,这样的等腰三角形有且只存在一个,请求出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com